-
Notifications
You must be signed in to change notification settings - Fork 1
Sampling uncertainty assessment
- What is sampling uncertainty?
- What is sampling uncertainty “not”?
- Do I really need to calculate the sampling uncertainty?
- Can WRES help me to calculate the sampling uncertainties?
- Is sampling uncertainty expensive to calculate?
- Can I calculate sampling uncertainties for summary statistics?
- Are there any limitations of the estimates?
- How does the stationary bootstrap work?
- Where can I learn more about the stationary bootstrap?
The sampling uncertainty of a statistic is the amount of uncertainty associated with a statistic when it is calculated from a limited sample. For example, when polling a population for their political or other views, the goal is to survey a representative sample of the population in order to provide some insight about the population as a whole (e.g., voters). Even when the sample is representative, the approximation of the population with a small sample creates some uncertainty, known as sampling uncertainty. Likewise, when evaluating models with a limited sample of model predictions, the evaluation statistics will contain sampling uncertainty. Practically speaking, this means that the “true” value of the statistic may lie within a range of possible values. Some values (or intervals of values) within this range may be more likely than others. In other words, there is a distribution of possible values or “probability distribution” associated with the statistic. For example, if a streamflow prediction model were calibrated to under-forecast streamflow by 5.0 cubic meters per second (CMS), on average, it’s possible that a limited sample would indicate a bias of 4.0 CMS or 2.7 CMS or even –23.8 CMS.
Evaluation statistics can be uninformative or misleading for a variety of reasons. An inadequate sample size is one of the most important reasons. However, there are other sources of uncertainty to consider. For example, the representativeness of a sample and its size are related concerns - the representativeness of a sample can increase as the sample size increases - but they are not exactly the same. If you were to collect a large sample of predictions and observations, perhaps spanning multiple decades, but focused on cool season conditions, that sample would be unlikely to represent warm season conditions adequately. Similarly, observations collected several decades ago may not be representative of current conditions if there were systematic changes in land-use, river regulation or climate over that period.
Even when you have a large and representative sample of predictions and observations, the observations may contain measurement or other errors that are non-trivial when compared to the prediction errors, particularly for extreme events, which are often of greatest interest.
In summary, sampling uncertainty is an important consideration when evaluating model predictions and, crucially, it is a tractable problem, i.e., there are practical ways to assess it. However, it is one of several considerations when designing evaluations that are informative.
Put simply, if the sampling uncertainties are large, your evaluations may be uninformative or, worse, misleading.
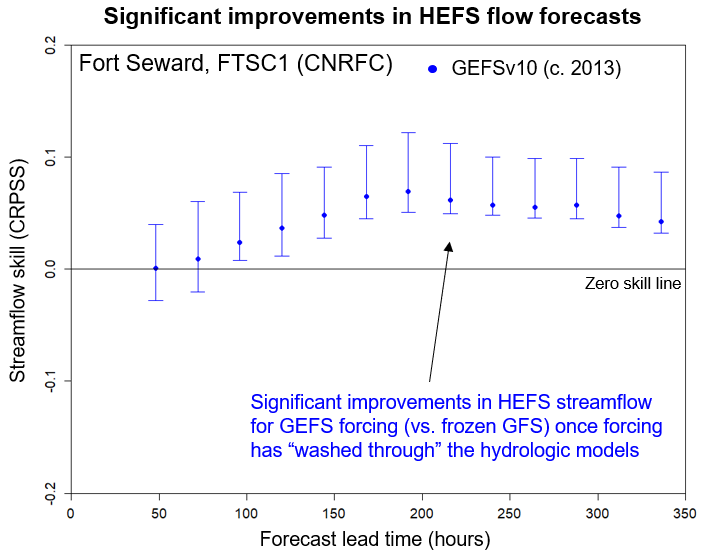
For example, consider the following evaluation of ensemble streamflow forecasts from the Hydrologic Ensemble Forecast Service (HEFS). The forecasts were evaluated for a 15-year period from 1985-1999 and for each of five, 3-year, sub-periods, in order to examine the variation in skill for different sub-samples of the overall dataset. As shown below, there is significant variation in skill within the overall period. To illustrate the practical significance of these variations, a further evaluation was conducted with a much older (c. 15-year) version of the meteorological forecast model used to force the HEFS. As indicated below, the improvement in skill from ~15-years of meteorological model development, which is represented by the red shaded area, is easily exceeded by the sampling variation between the 5-year sub-periods for the most recent model, which is represented by the blue area. In short, when using small datasets, the decision-making power of those datasets may be substantially weakened, to the extent that improvements from several years of model upgrades cannot be reliably detected, let alone a single model upgrade.

However, when using a large reforecast dataset (in this case, 1985-1999) and explicitly assessing the sampling uncertainties, there is a greater opportunity to show that the improvements in skill are statistically significant or that the model upgrades are providing value-for-money. As indicated below, when calculating the sampling uncertainties explicitly, it can be shown that a more recent version of the HEFS significantly outperforms a much older version. This improvement in skill generally accrues at later forecast lead times because the hydrologic response to meteorological forcing is lagged, i.e., takes some time to “wash through”, depending on basin characteristics (e.g., fast vs. slow responding).
Unless you calculate the sampling uncertainties explicitly, you are relying on experience to know when your statistics are informative. Can you rely on experience alone? Perhaps, if you have a lot of experience, but there are several factors that influence the amount of sampling uncertainty in a statistic, which can make it difficult to predict. In particular, the amount of sampling uncertainty will depend on the relationship between adjacent samples, assuming those samples are collected at adjacent times or locations. Consider a slow-responding river, where many samples of river stage are taken over a short period, say a few hours. Most likely, these samples will show very similar values. In general, adjacent samples have less unique insight or “statistical power” than samples taken far apart.
There are some “rules of thumb” to help understand this problem in particular cases. For example, consider the problem of estimating the degree of linear association or “cross-correlation” between model predictions and observations with a limited sample. If you have 100 samples to estimate the cross-correlation coefficient, but the samples are related to each other or “autocorrelated”, then you do not have 100 samples, in practice. Rather, you would have 100(1-0.9)/(1+0.9)=5.26 samples when the autocorrelation coefficient is 0.9, indicating that adjacent samples are very similar indeed. Clearly, an effective sample size of ~5 samples will produce an estimate with very large sampling uncertainty when compared to 100 independent samples.
There are several other factors that influence the amount of sampling uncertainty and, in general, it is safer to rely on explicit calculations than experience.
Yes. As of v6.16, the WRES has a feature that will calculate the sampling uncertainties for evaluation statistics using a “resampling” technique, known as the “stationary bootstrap”, How does the stationary bootstrap work?. The sampling uncertainties will be calculated on request. Here is an example of the declaration to use:
sampling_uncertainty:
sample_size: 1000
quantiles: [0.05,0.95]As noted above, every sample statistic has a “sampling distribution”. The sampling distribution identifies every possible value the statistic could take and the probabilities associated with them (or, strictly speaking, the probabilities associated with intervals of values). Consider a probability distribution curve, such as the normal distribution curve. When attempting to reproduce this distribution with a sample, you might draw a histogram of the sample, which approximates this curve. As the sample size increases, the approximation will improve and the histogram will become closer to the bell-shaped curve of the normal distribution. In this context, the sample_size represents the accuracy with which the sampling uncertainty is calculated. This is simply a parameter of the technique used to calculate the sampling uncertainty and should not be confused with the number of paired values in your dataset (which is also a “sample size” and partly determines the amount of sampling uncertainty).
As the sample_size increases, the quality of the estimate (of the sampling uncertainty) will improve, but this comes with a cost too. Each extra sample requires that your pairs of predictions and observations are resampled and the statistic computed afresh. Thus, when asking for a sample_size of 1000, this is akin to asking for the evaluation to be repeated 1000 times (not the portion concerned with gathering and reading data, but the metric calculations). In short, this number should be chosen carefully and guidance is provided in Is sampling uncertainty expensive to calculate?.
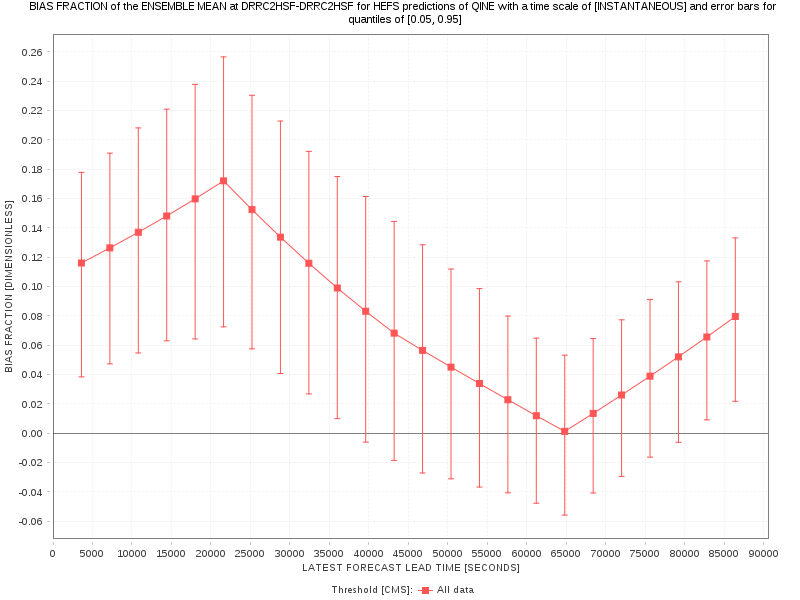
The quantiles is simply a list of values that are greater than zero and less than one. Each value corresponds to a position within the sampling distribution and can be used to declare the width of the error bars you’d like to calculate. For example, [0.05,0.95] will calculate the 0.05 and 0.95 quantile positions or 5th and 95th percentiles of the sampling distribution of each statistic. When choosing two or more quantiles and declaring graphics formats, these quantiles will be drawn as error bars in the graphics (when you declare more than two quantiles, the WRES will always draw the outermost quantiles). For example:
Yes, it is expensive to calculate and the cost increases proportionally with the sample_size or accuracy of the estimate. However, the problem scales better than linearly. For example, if your evaluation takes X amount of time, it will take much less than 500X time (on average) when adding the sampling_uncertainty option and declaring a sample_size of 500. Nevertheless, your evaluation may take ten or twenty times longer when calculating the sampling uncertainties and using a typical sample_size of, say, 1000 samples. In short, you should expect your evaluations to take significantly longer and you should be careful when setting the sample_size. If this value is too small, the estimates will not be reliable. If it is too large, the calculation will take too long and waste valuable resources.
What is a reasonable choice of sample_size? Technically, the WRES will allow you to declare a sample size that is between 2 samples and 100,000 samples. However, neither of these two extremes is recommended. In general, the value of each extra sample declines exponentially as the sample size increases. In other words, when you increase the sample_size from 100 to 101, the extra sample will have much greater value than increasing the sample_size from 5000 to 5001.
Based on theory and some experience, we recommend a sample size of around 1000 samples or larger, but you are unlikely to see very different results when increasing the sample size above 5000 samples. If there are differences, they are more likely to occur for the smaller subsamples or larger thresholds within your evaluation, such as flows above flood stage or other extreme events. Thus, a larger value of the sample_size (but probably not much larger than 5000) may be justified when considering extreme events.
No. Further information about summary statistics is available here: Evaluation summary statistics.
First, summary statistics are generally descriptive. In other words, they are not intended to make inferences about a broader population, they are simply describing a population. For example, an administrative region, such as a River Forecast Center (RFC), is composed of many hydrologic basins. When the evaluation statistics are summarized across all basins within an RFC, there is no uncertainty related to the sampling of basins because no basins are sampled (rather, the population of basins is being described).
Second, there are some cases where sampling uncertainties could apply. For example, you may want to summarize the evaluation statistics across a subset (sample) of features within a broader region. Alternatively, you may want to summarize the sampling uncertainties at individual locations, which originate from the finite sample of time-series pairs used in the evaluation (e.g., to answer the question: “what is the average amount of sampling uncertainty per location?”).
In practice, these sampling uncertainties are difficult to quantify because they require an understanding of (or assumptions about) the spatial relationships or “statistical dependencies” between geographic features. For example, while it is mechanically possible to compute an average across the confidence intervals generated for individual features, the resulting confidence interval would not be representative of the sampling distribution of the average of the underlying statistic because the statistics associated with the individual locations are most likely related to each other. A future version of the software may allow for these relationships to be quantified and hence the sampling uncertainties calculated.
The sampling uncertainties are estimated with a resampling technique, known as the stationary bootstrap, How does the stationary bootstrap work?. The technique itself makes several assumptions and its implementation within the WRES introduces several further assumptions for practicality. In general, the estimates should be reliable when the sample_size is adequately large and the assumptions are met. Equally, if the assumptions are not met, the estimates will be less reliable.
First, resampling a dataset cannot generate any more variability than the variability contained within the original dataset. Specifically, each resampled dataset is generated by resampling with replacement, which means that every original value is eligible to be resampled each time. This will not generate any new paired values, it will simply resample from the existing paired values. A particular resample may not contain every value from the original dataset (indeed, there would be no sampling uncertainty if it reproduced the original dataset each time). However, it is impossible for a resampled dataset to contain any values that are not in the original dataset. The most extreme observations and predictions in the original dataset will remain the most extreme observations and predictions in each resampled dataset (and they may not be contained in several of the resampled datasets). Consequently, when the sample sizes are very small (e.g., a few tens of samples or smaller), the statistics may have very large sampling uncertainties and, furthermore, the sampling uncertainties will be harder to estimate reliably. By definition, if a dataset contains a single sample, that dataset will contain zero sampling uncertainty according to resampling, which is clearly untrue. To mitigate this, you may choose to only calculate statistics when a minimum_sample_size is met. For example:
minimum_sample_size: 30
sampling_uncertainty:
sample_size: 1000
quantiles: [0.05,0.95]In this case, a statistic will not be calculated unless the sample size is at least 30 pairs (for dichotomous statistics, this means 30 occurrences or 30 non-occurrences, whichever is smaller).
Second, the stationary bootstrap will not estimate any uncertainties that are unrelated to sampling, such as measurement or observational errors. Similarly, it will not correct for any mistakes in the design or interpretation of your evaluation. For example, if the statistical behavior of the predictions or observations (or their combination) changes systematically across the sample (e.g., from earlier years to later years due to climate change, land-use change, changes in river regulation or any other systematic causes), then you cannot rely on the estimates of sampling uncertainty, or indeed the evaluation more generally, as being representative or informative for current operations. Furthermore, the “stationary bootstrap” assumes that the statistics of the predictions and observations and their combination (pairs) do not change significantly or systematically over time. Failing to adhere to these assumptions will not prevent the WRES from providing you with estimates, but the quality of these estimates may be poor.
Third, when resampling the paired data, the WRES invokes several “special” assumptions. These assumptions are not prescribed by the “stationary bootstrap” technique, but are adopted by WRES for simplicity:
- That the time-series have a regular structure, meaning a consistent timestep between values. When resampling values, they are sampled to account for the temporal relationships (”statistical dependencies”) between values. As noted earlier, the relationships between values in space and time can have a dramatic impact on the sampling uncertainty and the technique used to account for these relationships depends on a regular structure. If the time-series are irregular, whether inherently or due to missing data, the estimates may not be reliable.
- The WRES calculates evaluation statistics for “pools” of data that are declared by a user. For example, an evaluation of forecasts will typically contain a separate “pool” for each forecast lead time. When a pool contains multiple forecast lead times, the resampling occurs for each lead time separately. In other words, when resampling values for a given forecast lead time, only those values with a corresponding lead time are eligible for resampling.
- When a pool contains multiple locations, the resampling assumes perfect statistical dependence between locations. In other words, if the pool contains samples for two locations, DRRC2 and DOLC2, randomly resampling a value at 2023-10-27T12:00:00Z from location DRRC2 means that the correspondingly timed value will be (deterministically) resampled from location DOLC2. This is a conservative assumption because the sampling uncertainties will generally increase as the relationship between samples increases. In short, if you aggregate many locations within a single pool and those locations are far apart, the sampling uncertainties may be unreliable (overestimated).
The technique implemented in WRES is adapted from Politis, D. N. and Romano, J. P. (1994) (see Where can I learn more about the stationary bootstrap?.
Consider a time-series, with valid times, v=1,...,V, and lead durations, w=1,...,W. The time-series values always contain pairs of predictions and verifying observations, which are omitted from this notation. Each time-series contains a reference time or issued time (we assume one, for simplicity) and the difference between the issued time and each valid time is a lead duration. When the predicted values are observations, simulations or analyses, each lead duration is zero: t 1,0,…,t V,0 because the issued times and valid times are identical. When the predicted values are forecasts, each lead duration increments in a regular sequence: t 1,1,…,t V,W.
Evaluation statistics are always calculated from a “pool” of up to T time-series. For example, consider a sequence of time-series, such that each issued time is separated by one time-step (i.e., one gap between consecutive valid times):
t1 = t1,1,…,tV,W
t2 = t2,1,…,tV+1,W
.
.
.
tT = tT,1,…,tVT,W
The evaluation statistics are computed from all of the values (pairs of predictions and observations) within this pool. Typically, when evaluating forecasts, each pool will contain a time-series with a single (fixed, constant) lead duration because forecast quality generally declines as the lead duration increases. However, in principle, a pool may contain time-series with more than one lead duration and, hence, an incrementing sequence of valid times in each time-series.
The stationary bootstrap is a resampling technique. Resampling works by generating an “alternative” dataset or “realization” of the original dataset, and repeating this up to R times. The evaluation statistics are then computed separately for each of these R realizations and gathered together to approximate the sampling distribution of each evaluation statistic. For example, when R=500, there are 500 samples from the sampling distribution of each evaluation statistic. These distributional samples can be further summarized. For example, by selecting the 5th and 95th percentiles from the samples, it is possible to draw error bars around each statistic, which are akin to 5-95 confidence intervals.
The goal, then, is to generate up to R realizations of the pooled data, r=1,...,R. The rth realization of the first time-series can be denoted: t r 1 = t r 1,1,…,t r V,W. Thus, for example, the first realization of a pool can be written as:
t11 = t11,1,…,t1V,W
t12 = t12,1,…,t1V+1,W
.
.
.
t1T = t1T,1,…,t1VT,W
To generate this realization, the stationary bootstrap uses the following sequence:
- Sample the first (paired) value in the first time-series, t 1 1,1 by randomly selecting a value from the original time-series values, (t 1,1,…,t T,1), and denote that sample t v,1. In this way, the only values from the original dataset that are eligible for resampling are those values with
w=1. ; - If the first time-series contains a second index, sample the second index as value t v+1,2 from the original pool with probability
1-pand, with probability,p, sample the value randomly from (t 1,2,…,t T,2). If the first time-series does not contain a second index, proceed to step (4); - Repeat step (2) for each additional index within time-series t 1 1, substituting t v,1 with the last sampled index each time;
- With probability
1-p, sample the first value in the second time-series, t 1 2,1, as the value t v+1,1 from the original time-series and, with probabilityp, sample the value randomly from (t 1,1,…,t T,1); and - For each new time-series, repeat step (4), followed by steps (2) and (3) until the value t 1 VT,W has been sampled.
The sequence is then repeated for each new realization, until r=R.
When index t v+1,w exceeds the largest index in the corresponding time-series, then the resampling is started afresh at index t 1,w, i.e., circular sampling is employed. The probability p is determined by the separation distance or “lag”, expressed in units of time-steps, at which the time-series values are no longer correlated or “statistically dependent” on each other, where p=1/lag. This lag distance is estimated from the autocorrelation function using the procedure described in Politis and White (2004) and Patton et al., (2008) (see Where can I learn more about the stationary bootstrap?). The resampling procedure assumes regular time-series or, more specifically, time-series with a fixed time-step between adjacent valid times. However, the offset between issued times (or between the first valid time in adjacent series) can be a multiple of the timestep and the transition probability, p, in step (4) is adjusted accordingly.
When a pool contains time-series with multiple spatial locations, the locations are sampled with perfect statistical dependence across locations, i.e., the time index sampled for one location is the time index from which all other locations are sampled, deterministically.
- Politis, D. N. and Romano, J. P. (1994). The Stationary Bootstrap. Journal of the American Statistical Association, 89:428, 1303-1313.
- Politis, D.N., and White, H. (2004). Automatic block-length selection for the dependent bootstrap. Econometric Reviews, 23(1):53-70.
- Patton, A. Politis, D.N. and White, H. (2008). CORRECTION TO ‘Automatic Block-Length Selection for the Dependent Bootstrap’ by D.N. Politis and H. White. Econometric Reviews, 28(4):372-375.
The WRES Wiki
-
Options for Deploying and Operating the WRES
- Obtaining and using the WRES as a standalone application
- WRES Local Server
- WRES Web Service (under construction)
-
- Format Requirements for CSV Files
- Format Requirements for NetCDF Files
- Introductory Resources on Forecast Verification
- Instructions for Human Interaction with a WRES Web-service
- Instructions for Programmatic Interaction with a WRES Web-service
- Output Format Description for CSV2
- Posting timeseries data directly to a WRES web‐service as inputs for a WRES job
- WRES Scripts Usage Guide