--{{0}}--
Auch wenn es sich vielleicht technisch anhört und sehr oft kompliziert beschrieben wird, so ist eine Regelung ein sehr altes Konzept, das schon weit vor dem Menschen von Mutter-Natur genutzt wurde, damit ihre Organismen sich auf Änderungen der Umgebung anpassen können.
--{{1}}--
Damit ist hier jedoch nicht die Evolution gemeint, sondern die vielen kleinen Abläufe, die im inneren eines jeden Organismus stattfinden, wie die Konstanthaltung der Körpertemperatur oder des Blutzuckerspiegels, die Anpassung der Pupille and Helligkeitsänderungen, das Halten den Gleichgewichts, bei einfachen Organismen können sogar deren Verhaltensweisen leicht mit regelungstechnischen Mechanismen erklärt werden.
--{{2}}--
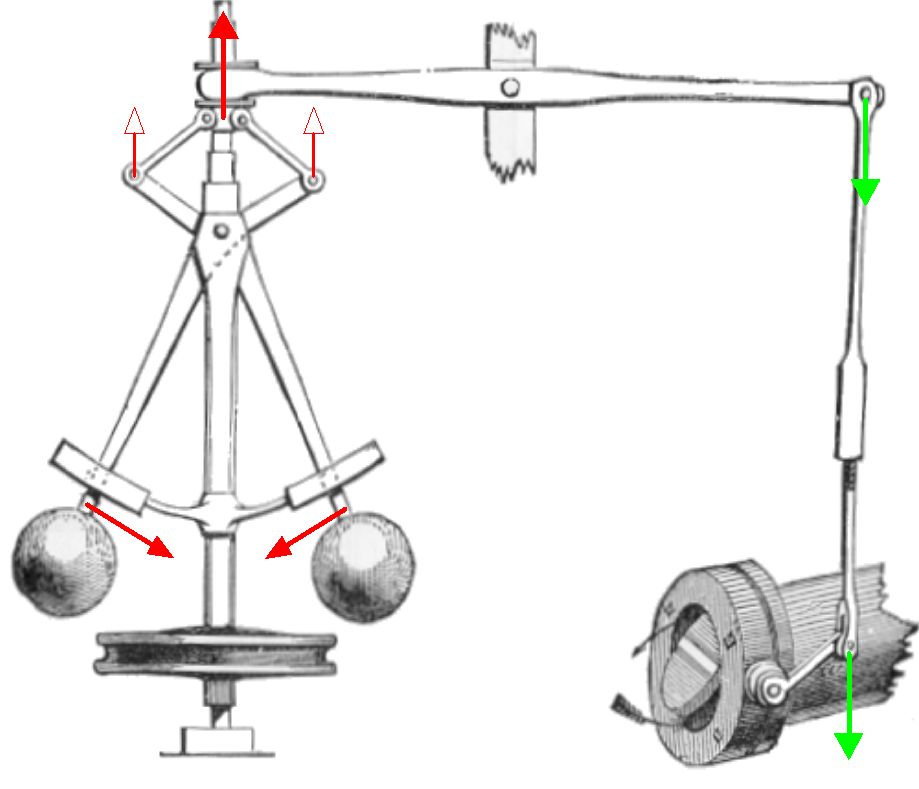
Die ersten Menschen, die dieses Prinzip nachweislich, erkannten und nutzten waren, nicht wie so oft erwähnt, die Ingenieure des 17. und 18. Jahrhunderts wie zum Beispiel James Watt1 mit seinem Fliehkraftregler, sondern Mechaniker der griechischen Antike, wie Ktesibios, Philon und Heron, die Schwimmerregelungen erdachten, wobei die ursprüngliche Anwendung im Bau von Wasseruhren lag.
Also was ist nun eine Regelung?
--{{1}}--
Die Abbildung zeigt den typischen Aufbau eines einschleifigen Regelkreises, hierbei wird im Gegensatz zu einer Steuerung (die hier nicht behandelt werden soll) mit dem Prinzip der Rückkopplung (Feedback) gearbeitet. Dabie wird die zu regelnde Größe (Ist-Wert) fortwährend überwacht und mit einer anderen Größe, der Führungsgröße (Soll-Wert), verglichen. Die Regelgröße kann durch verschiedene externe Kräfte (Regelstrecke) gestört werden und damit von der Führungsgröße abweichen.
--{{2}}--
Ein Vorteil gegenüber der Steuerung ist, dass diese störenden Kräfte nicht im Einzelnen erfasst werden müssen (eventuell ist dies gar nicht möglich), vielmehr wird nur der Unterschied zwischen Regel- und Führungsgröße (Ist- und Soll-Wert) als Gesamtfehler (oder Regelabweichung) betrachtet. In Abhängigkeit dieses Gesamtfehlers wird versucht, eine dritte Größe (Stellgröße) in geeigneter Weise zu beeinflussen, um die Regelabweichung zu minimieren.
--{{3}}--
Was hier noch nicht erläutert wurde, das ist die Regeleinrichtung. Dabei handelt es sich um den eigentlichen Regler, also P, I, D und die die Kombinationen daraus, sowie weiter Arten. In den folgenden Abschnitten werden wir die verschieden Reglerarten noch näher erläutern.
Störgröße -+
d(t) |
Führungsgröße Regelabweichung Stellgröße v
w(t) e(t) +------------------+ u(t) +--------------+
---------> o ------> | Regeleinrichtung |------->| Regelstrecke |----- o ----->
+------------------+ +--------------+ |
^ |
|___________________________________________________________|
(Rückführung der Messgröße)
--{{4}}--
Betrachten wir das Beispiel nochmal kurz aus den Blickwinkel eines Autofahrers auf der Autobahn (ohne Abstandsautomatik, CruiseControl, etc.). Der Fahrer muss die Geschwindigkeit seines PKWs ständig an die verschiedenen Richtgeschwindigkeiten und die aktuelle Verkehrssituation anpassen. Die Führungsgröße steht hier für die vorgegebene Richtgeschwindigkeit, die Regelgröße steht für die Geschwindigkeit des Fahrzeugs. Über das Tachometer kann der Autofahrer ständig vergleichen, wie sich seine aktuelle Geschwindigkeit von der Richtgeschwindigkeit unterscheidet (Rückkopplung). Ausgehend von diesem Geschwindigkeitsunterschied beschleunigt oder bremst der Autofahrer, die Stellgröße, mit der er auf die Geschwindigkeit einwirkt, ist sein Fuß auf dem Gaspedal. Störkräfte könnten in diesem Beispiel die verschiedenen Anstiege oder Kurven der Fahrstrecke, aber auch andere Autofahrer sein. Aufgrund der Störungen oder der Änderung der Richtgeschwindigkeit ist der Fahrer immer wieder gezwungen, seine Geschwindigkeit anzupassen (Regeln). Wie jeder Fahrer auf das Gaspedal tritt, eher langsam und zaghaft oder schnell und ruppig, wird durch seine Art und Regelparameter bestimmt.
--{{0}}--
Je nach Regelungsaufgabe gibt es eine Vielzahl verschiedener Typen von Regelungen, die ihrerseits spezifische Vor- und Nachteile besitzen. Durch die Kombination verschiedener Regler lassen sich wiederum andere Regler finden mit wieder anderen Eigenschaften (in diesem Zusammenhang spricht man auch Reglern, bestehend aus Regelgliedern). Welcher der ideale Regler für eine gegebene Regelungsaufgabe ist, lässt sich meist nur schwer ermitteln. Man benötigt zum Teil genaue Kenntnis der Regelstrecke, erschwerend können noch Güteforderungen1 hinzukommen und wurde schließlich ein Regler gefunden, so müssen noch dessen Parameter angepasst werden.
+-----> Prozess (Aufgabe) -----+
| |
| v
Aktuatoren Sensoren
^ |
| |
+---------- Regler??? <--------+
--{{1}}--
Die wichtigsten klassischen Regler sollen im Folgenden kurz vorgestellt werden. Dazu zählen Proportional-, Integral- und Differenzialregler.
--{{0}}--
In ihrer einfachsten Form spricht man von einem verzögerungsfreien P-Regler,
dabei verändert sich der Wert der Stellgröße
--{{1}}--
Der statische Faktor
--{{2}}--
Der Vorteil des P-Reglers liegt in der schnellen Reaktion auf Änderungen der
Regelgröße. Des Weiteren neigen P-Regler bei einem zu hohen Wert für
--{{0}}--
Beim integralwirkenden Regler (I-Regler) wird die Stellgröße
--{{1}}--
Das verzögerungsfreie I-Glied wird durch die Differenzialgleichung mit
{{1}} $$ u(t) = \frac{1}{T_I} * \int_{0}^{t} e(t) dt + u_{0} $$
--{{2}}--
Integralwirkende Regel sind im Vergleich zu anderen Reglern zwar langsamer, haben jedoch den Vorteil, dass sie eine Abweichung von Soll- zu Regelgröße vollständig eliminieren können.
--{{0}}--
Bei differenzialwirkenden Regelungsgliedern (D-Regler) bestimmt die Änderung der Regelabweichung die der Stellgröße. Ein verzögerungsfreies D-Glied ist wie folgt definiert:
--{{1}}--
Reale physikalische Systeme lassen sich praktisch nicht mit Reglern, bestehend aus einem verzögerungsfreien D-Glied, regeln, da die Stellgröße hier nur mit einem Diracimpuls antwortet. Das heißt, die Stellgröße steigt zu Beginn unverhältnismäßig stark und geht dann bei konstanter Regeldifferenz gegen null. Aus diesem Grund müssen D-Glieder auch mit anderen Regelgliedern kombiniert werden, vorzugsweise mit P-Reglern, sie werden aber auch zur Stabilisierung von I-Reglern höherer Ordnung eingesetzt. Ein Nachteil aller Regler mit D-Anteil ist die Unruhe bei verrauschtem Eingangssignal. Das Rauschen wird verstärkt und über die Stellgröße wieder in den Regelkreis, was unter anderem auch zu starken Schwingungen der Stellgröße führen kann.
--{{0}}--
Die folgenden Seiten sollen den Schrecken etwas mindern und zeigen, wie einfach man Regler in einem Programm implementieren kann.
--{{0}}--
Auch wenn die Formeln auf den vorhergehenden Seiten etwas kompliziert aussahen, ist, deren Diskretisierung um ein Vielfaches einfacher und man benötigt kein CAS1(Computer Algebra System) um diese in Software auszudrücken.
--{{1}}--
Die Diskretisierung eines P-Reglers sollte trivial sein und für jeden ersichtlich.
{{1}} $$ u(t) = K_P * e(t) $$
--{{2}}--
Die Gleichung für den Integral-Regler sieht schon etwas komplizierter aus, für
den Anfang. Wenn wir von einer konstanten Abtastzeit ausgehen, die nicht gegen
null strebt, dann das Integral auch durch eine einfache Summe ausgedrück werden.
Wenn wir von dem Startpunkt
{{2}}
$$ u(t) = K_I * \sum^{t}_{t = 0} e(t) + u(0) ,
\text{mit } K_I = \frac{1}{T_I} $$
--{{3}}--
Zu guter Letzt, die diskrete Formel für den D-Regler. Um das ganze noch ein
wenig zu vereinfachen, setzen wir im Folgenden
{{3}} $$ u(t) = K_D \frac{e(t) - e(t-1)}{T} $$
--{{0}}--
Ein PID-Regler kann einfach durch Addition der einzelnen Regelglieder gebildet
werden und die unterschiedlichen Faktoren (
$$ u(t) = \underbrace{K_P * e(t)}{\text{Proportionalteil}} + \overbrace{K_I * \sum^{t}{t = 0} e(t) + u(0)}^{\text{Integralteil}} + \underbrace{K_D * (e(t) - e(t-1))}_{\text{Differenzialteil}} $$
--{{1}}--
Üblicherweise und wie der Name schon sagt, geht man bei einem PID-Regler davon aus, dass der P-Anteil am höchsten ist, somit wird schnell auf den Fehler reagiert. Den zweithöchsten Einfluss hat der I-Anteil, der dafür sorgt, dass der Regler nicht schwingt und den Soll-Wert auch exakt erreicht. Das schwächste Glied im Bunde ist der D-Anteil, der bei starken Änderungen des Fehlers für eine schnelle Reaktion sorgen soll, jedoch mit Rauschen sehr viele Probleme hat.
{{1}} $$ K_P \gt K_I \gt K_D $$
--{{0}}--
Das folgende Programm soll demonstrieren wie einfach man selber eine Regelung
samt Regelstrecke implementieren kann. Alle wichtigen Paramter sind im Kopf des
Programms gesetzt, wobei zu beachten ist, das die integral (Ki) und
differenzial (Kd) hier noch ausgeschaltet sind. Wenn ihr ein wenig mit den
Wert für Kp experimentiert, dann werdet ihr schnell merken, dass dieser Regler
allein sehr unbrauchbar ist und für große Werte schnell Überschwingt und bei
allen kleineren Werten sein Soll niemals erreicht. Er ist deshalb nur in einigen
Spezialfällen nützlich. Versucht deshalb auch den I-Anteil langsam zu erhöhen
und nehmt dann den D-Anteil hinzu. Beachtet, wie sich die unterschiedlichen
Regler einem festen Wert annähern.
let w = 1; // Führungsgröße (Sollwert)
let u = 0; // Stellgröße (Druck auf das Gaspedal)
let Kp = 0.6; // proportional Faktor
let Ki = 0; // integral Faktor (ausgeschaltet)
let Kd = 0; // differenzial Faktor (ausgeschaltet)
let e_now = 0; // Regelabweichung e(t)
let e_old = 0; // Regelabweichung e(t-1)
let e_sum = 0; // Summe über allen Fehlern
// Speicher für den ist-Wert als Ergebnis der Regelstrecke
let ist = 0;
// eine einfache (konstante) Regelstrecke für den Anfang
function Regelstrecke(t, u) {
if (t < 50)
return 0 + u;
else
return 1 + u
}
// Taktgeber
for(let t = 0; t < 100; t++) {
ist = Regelstrecke(t, u);
let e = w - ist; // Feedback ... Berechnung des Gesamtfehlers
e_old = e_now;
e_now = e;
e_sum = e_sum + e_now;
// Bestimmung der neuen direkten Stellgröße
u = Kp * e_now + Ki * e_sum + Kd * (e_now - e_old) ;
print("t: "+t+" soll:"+w+" ist:"+frmt(ist,12)+" e:"+frmt(e,12));
update(t, w, ist); // plotten der Ergebnisse im Diagram
wait(50); // verzögert den Schleifendurchlauf um 50ms
}@eval(PID-Regler)
--{{1}}--
Wenn ihr ein wenig mit unterschiedlichen Regelstrecken experimentiert, dann
werdet ihr schnell herausfinden, dass ein richtig eingestellter PID ein sehr
allgemeiner und robuster Regler ist. Ihr könnt aber auch versuchen eine Funktion
für den Soll-Wert w zu definieren, der sich in Abhängigkeit von t auch
verändert.
{{1}}
function Regelstrecke(t, u) {
if(t < 33)
return 0 + u;
else if(t < 66)
return t + u;
else
return t * 0.1 + u;
}