并查集主要处理的问题是连接问题。主要回答的是一个网络当中两个节点是否连接的问题。尤其实在大数据的情况下,并查集的使用显得尤为重要。对于一组数据主要支持两个动作。
- union(p, q) // 连接两个元素
- isConnected(p, q) // 查看是否连接
从上面我们也就可以得出并查集的接口函数 程序实现:
public interface UF {
int getSize();
boolean isConnect(int p, int q);
void unionElements(int p, int q);
}我们在实现的时候采用数组的形式进行实现。
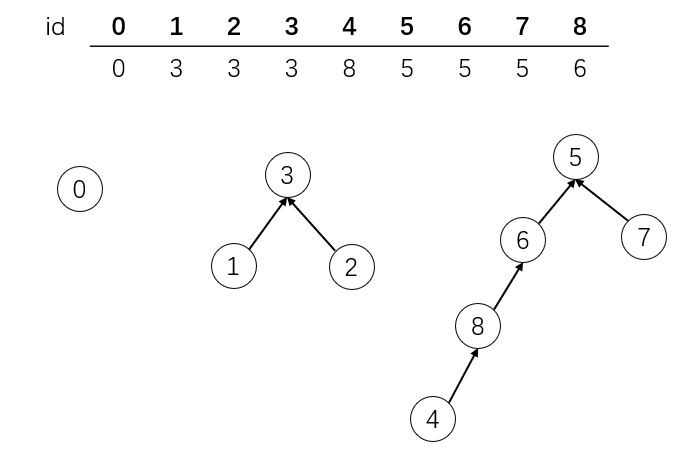
从图中我们看出来,id代表我们要查询的索引,下面的值代表了类别。0-4为一类,5-8为一类。设计的主要方法主要是判断是否连接和让两个节点进行连接。
这个版本中,判断两个节点是否连接,直接判断节点索引对应的值是否相同。之所以使用find函数是因为我们需要每次查询的时候都要判断我们的索引是否越界。 程序实现:
private int find(int p) {
if (p < 0 || p >= id.length)
throw new IllegalArgumentException("p is out of bound");
return id[p];
}
@Override
public boolean isConnect(int p, int q) {
return find(p) == find(q);
}我们这里需要注意,我们连接两个元素,并不仅仅是索引的两个值进行相同。我们需要让他们这一类全部相同。例如,针对上面的图片结构,如果我们unionElement(0, 7)。那么所有的值均要变为0。 程序实现:
@Override
public void unionElements(int p, int q) {
if (isConnect(p, q)) // 先判断是否连接
return;
for (int i = 0; i < id.length; i++) //遍历整个数组继续两个节点的所以伴随节点全部相同
if (id[i] == id[q])
id[i] = id[p];
}我们发现,版本一的不足之处就在于连接两个元素的时间复杂度为O(N)级别,需要遍历整个数组。
我们这里优化的方式就是采用树结构。我们这里的树结构同以往不一样。向二分搜索树的树结构都是父节点指向子节点。但是在并查集里面我们需要设立一个子节点指向父节点的树结构。
一个树即为一类,我们再进行连接的时候,只需要将他们的父节点连接在一起就可以了。这里父亲节点的方式是参数在前的节点去链接参数在后面的节点。
我们这里依然采用数组进行实现。
如果id和值相同,那么该节点为根节点 我们可以根据数组来写出下面的树结构。例如,我们要查找节点8的父亲节点
- id = 8,对应的值为 6
- 我们再去查找id = 6 的值,对应的值为 5
- 再去查找id = 6 的值,对应的值为 5
- 再去查找id = 5 的值,对应的值为 5。和id相同即为父亲节点
我们在初始化数组的时候,让每一个节点都是根节点,也就是均等于自己的id。 程序实现:
public UnionFind_v2(int size) {
parent = new int[size];
for (int i = 0; i < parent.length; i++)
parent[i] = i;
}在这里我们需要找到对应节点的根节点,判断他们根节点是否相同。
例如:针对上面的结构,我们我们判断isConnect(4, 7)。我们发现节点4和7对应的根节点都为5,所以我们是连接的关系。
创建私有函数,用来查询节点的父亲节点。 程序实现:
private int findParent(int id) {
if (id < 0 || id >= parent.length)
throw new IllegalArgumentException("id is out of bound");
while (parent[id] != id) { //结束条件id和值相同,即为根节点
id = parent[id];
}
return id;
}
@Override
public boolean isConnect(int p, int q) {
return findParent(p) == findParent(q);
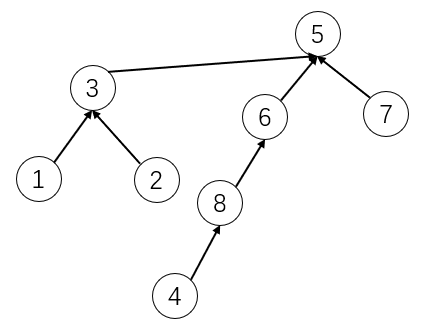
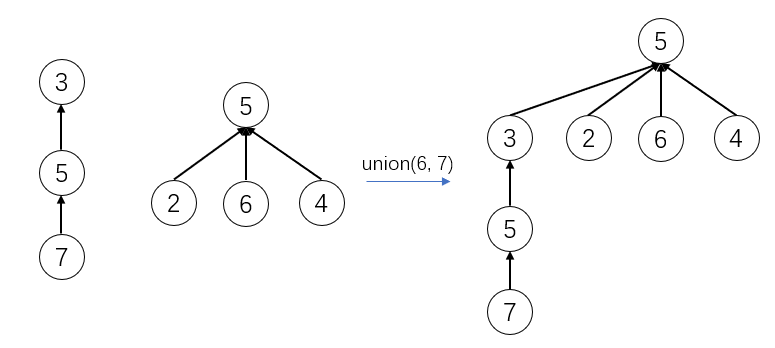
}对于union(int m1, int m2),我们规定让m1的根节点去连接m2。我们一上面的树结构为例子,如果执行union(1, 8)。那么树结构就会变为
1的根节点3去指向8的根节点5。
程序实现:
@Override
public void unionElements(int p, int q) {
if (isConnect(p, q))
return;
int parent_p = findParent(p);
parent[parent_p] = findParent(q);
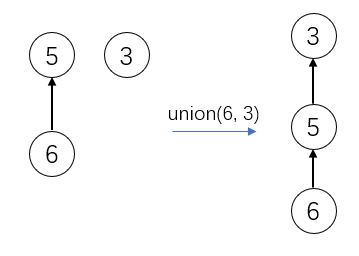
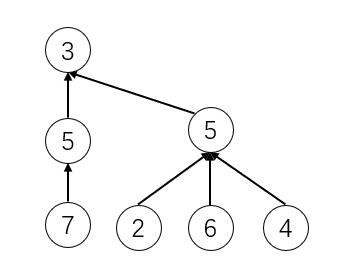
}在前面的例子中,我们人为规定前面的参数指向后面的参数,而没有进行优化。在下面例子中我们看到,如果执行union(6, 3)
我们知道树结构的时间复杂度是跟树的高度相关的。如果按照版本二方式操作的话,导致树的高度变高。实际中我们是希望的得到这种的结果:
我们希望的是让包含节点少的树结构去指向节点多的树结构。
针对这种情况,我们引入一个新的数组,用来保存根节点下的所包含的节点数量
程序实现:
public UnionFind_v3(int size) {
parent = new int[size];
sz = new int[size];
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
sz[i] = 1; //初始根节点个数均为1
}我们依然引入私有函数用来查找id所对应的根节点。这里和版本二相同。 程序实现:
private int findParent(int id) {
if (id < 0 || id >= parent.length)
throw new IllegalArgumentException("id is out of bound");
while (parent[id] != id) {
id = parent[id];
}
return id;
}
@Override
public boolean isConnect(int p, int q) {
return findParent(p) == findParent(q);
}和版本二不用,我们需要判断待两个节点的根节点的子节点个数。用小的树结构指向大的树结构。最后需要对size进行更新。
程序实现:
@Override
public void unionElements(int p, int q) {
int pRoot = findParent(p);
int qRoot = findParent(q);
if (isConnect(p, q))
return;
// 用来决定是谁指向谁
if (sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot]; //更新size
}
else{
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
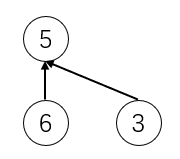
}其实对于版本三的优化并不彻底。其实我们真正需要的是降低树的高度,size小并不代表高度低。例如下面这种结构。
按照我们版本三的思路,节点3去指向节点5,反而导致树结构高度为4。如果我们让高度低的去指向高度高的,那么树的高度将不会增加。具体可以参照下图:
如果两个高度相同的进行连接,那么高度只会增加一。具体的话小伙伴可以自己画一画。
增加rank数组用来保存节点的高度
public UnionFind_v4(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
rank[i] = 1; //初始化高度为1
}
}和以前一样增加私有函数用来查看根节点,同之前版本相同。 程序实现:
private int findParent(int id) {
if (id < 0 || id >= parent.length)
throw new IllegalArgumentException("id is out of bound");
while (parent[id] != id) {
id = parent[id];
}
return id;
}
@Override
public boolean isConnect(int p, int q) {
return findParent(p) == findParent(q);
}连接两个节点主要是对高度的判断以及更新操作。 程序实现:
@Override
public void unionElements(int p, int q) {
int pRoot = findParent(p);
int qRoot = findParent(q);
if (isConnect(p, q))
return;
// 高度不同的连接不会增加树的高度
if (rank[pRoot] < rank[qRoot])
parent[pRoot] = qRoot;
else if (rank[pRoot] > rank[qRoot])
parent[qRoot] = pRoot;
else{
parent[qRoot] = pRoot;
rank[pRoot]++; //相同高度增加1
}
}小伙伴可能会疑问,为什么还有优化的方式呀,树的高度已经最优化了,为什么还会有高度上的优化。
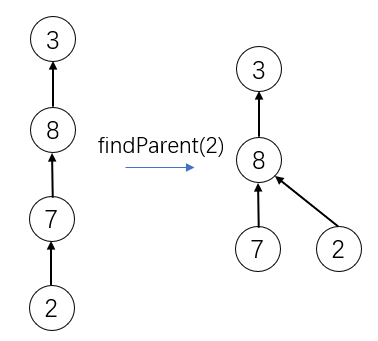
其实,并查集的这种数据结构,对于树的结构本身是什么样子的,我们并不关心,只要是同一个树,那么它的他们的全部节点就是一类。所以我们可以任意修改树的结构,修改的方式就是在查询操作的时候对树在高度上进行压缩。 操作:
parent [ id ] = parent [ parent [ id ] ]
也就是节点向上移动一位
我们对版本四的代码不需要其他操作,只要增加一行代码即可。也就是私有函数的findParent()中增加一行,其他的完全一样。 更改代码:
private int findParent(int id) {
if (id < 0 || id >= parent.length)
throw new IllegalArgumentException("id is out of bound");
while (parent[id] != id) {
parent[id] = parent[parent[id]]; //增加一行代码
id = parent[id];
}
return id;
}更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。