-
-
Notifications
You must be signed in to change notification settings - Fork 1
Fastest Method to Print Integers and Floating point Numbers
Notice of Change: This algorithm just got renamed to the Puff Algorithm, a new faster and more portable early beta version algorithm has been released and the benchmarks listed are of the older slower larger soon to be depreciated Script ItoS, but they will more than likely be the same. 2018/10/21
This document contains a method to increase the performance of Integer-to-String Algorithm (ItoS) and floating-point-to-string Algorithm (FtoS) conversion using three methods that combine to create the Puff algorithm, simultaneously the world's fast ItoS and an incrementally faster version of the Grisu FtoS. Grisu is the world's fastest FtoS that replaced the Dragon4 algorithm. Grisu is a cartoon dragon, so Puff, as in Puff the Magic Dragon, is an appropriate name an improved version of Grisu[A].
The primary performance boost from Puff comes from performing manual modulo to avoid "throwing the baby out with the bath water", and grouping decimals into groups of 8 in order to avoid half the division instructions of the hardware modulo method and one less division instruction from applying the manual modulo to the unrolled modulo 100 loop. Additional optimizations that more so affect the conversion of small integers include a faster printing the Most Significant Decimal (MSD) using bit shifting to find the power of 10. One pleasant side effect of the converting 8 decimals at a time is that the same algorithm can then be used to convert both 32-bit and 64-bit integers with a single C++ templated function, and we get an extra optimization through packing and cache aligning the Lookup Tables for both the ItoS and FtoS that also allows us to use a single templated C++ function with Flywheel Design Pattern to print any sized IEEE 754 floating-point number in ASCII/UTF-8, UTF-16, or UTF-32.
This algorithm is an open-source research-paper-driven innovation, meaning that the algorithm did not exist when the article was created and was actually created through a wiki. From time to time the wiki may get updated until there is no possible way to optimize the innovation so please check back updates to https://github.com/kabuki-starship/kabuki-toolkit/wiki/Fastest-Way-to-Print-Integers-and-Floating-point-Numbers and please submit any errors to Cale McCollough at [email protected].
-
Overview
- Content Table
- Author
- License
- State of the Art
- Innovations
- Puff Algorithm
- Conclusion
Copyright 2018 (C) Cale McCollough and contributors. All rights reserved (R).
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License here.
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
In order to print floating-point numbers you must also print integers. The fastest method to print floating-point numbers is the Grisu2 algorithm, and the algorithm works faster by printing two integers at a time.
The fastest way to convert from an integer to a string (ItoS) is using modulo 100 arithmetic and a lookup table string of ASCII bytes for numbers 00 through 99.
static const char kDigits0To99[200] = {
"00010203040506070809"
"10111213141516171819"
"20212223242526272829"
"30313233343536373839"
"40414243444546474849"
"50515253545556575859"
"60616263646566676869"
"70717273747576777879"
"80818283848586878889"
"90919293949596979899"
};Conceptually we only deal with the unsigned case because signed is just a special case that adds a single ASCII '-' character. We first start by finding the string length using a binary search pattern with base 10 numbers.
inline int StringLength(uint32_t value) {
if (value < 10) return 1;
if (value < 100) return 2;
if (value < 1000) return 3;
if (value < 10000) return 4;
if (value < 100000) return 5;
if (value < 1000000) return 6;
if (value < 10000000) return 7;
if (value < 100000000) return 8;
if (value < 1000000000) return 9;
if (value < 10000000000) return 10;
if (value < 100000000000) return 11;
return 12;
}The algorithm then follows by a loop that performs modulo 100 arithmetic and another that follows to take care of the remaining value.
enum { kSize = 16 };
char buffer[kSize];
char* cursor = buffer + size - 1;
while(value>=100) {
int hundreds = value % 100;
value /= 100;
// Please note we're printing backwards hence - 1.
*(uint16_t*)(cursor - 1) = kDigits0To99[hundreds];
c -= 2;
}
while(value > 0) {
*cursor-- = '0' + (value % 10);
value /= 10;
}The fastest algorithm to print floating-point numbers is the Grisu2 algorithm outlined in the research paper Printing Floating-point Numbers Quickly and Accurately by Florian Loitsch which can be found at:
It is very complicated math and it is not needed to repeat that work of art, but the Puff ItoS is easily applied to the Grisu2 algorithm:
struct diy_fp {
uint64_t f;
int32_t e;
};
void digit_gen(diy_fp Mp, diy_fp delta, char* buffer, int* len, int* K) {
uint32_t div;
int32_t d, kappa;
diy_fp one;
one.f = ((uint64_t)1) << -Mp.e;
one.e = Mp.e;
uint32_t p1 = (uint32_t)(Mp.f >> -one.e);
uint64_t p2 = Mp.f & (one.f - 1);
*len = 0;
kappa = 10;
div = 1000000000;
while (kappa > 0) {
d = p1 / div;
if (d || *len) buffer[(*len)++] = '0' + d;
p1 %= div;
div /= 10;
kappa--;
if ((((uint64_t)p1) << -one.e) + p2 <= delta.f) {
*K += kappa;
return;
}
}
do {
p2 *= 10;
d = (uint32_t)(p2 >> -one.e);
if (d || *len) buffer[(*len)++] = '0' + d;
p2 &= one.f - 1;
kappa--;
delta.f *= 10;
} while (p2 > delta.f);
*K += kappa;
}Puff innovates over the prior art by making a single C++ templated class that can print UTF-8, UTF-16, and UTF-32 using three optimizations: Optimized Lookup Tables for printing both integers and floating-point numbers, faster conversion of the Most Significant Decimal, and optimized Modulo 100 arithmetic.
x86 CPUs allow for unaligned memory access but it's slow for older CPUs and other CPUs, such as ARM Cortex-M0, do not allow for unaligned memory access. C++ does not guarantee word-alignment of static const strings. An easy solution is to convert the digits 00 through 99 into 16-bit types for 00, 01, .., 99. This consequentially makes the code easier to read and lets the compiler do the bit shift right/left optimization to multiply/divide by 2.
static const uint16_t kDigits00To99[100] = {
0x3030, 0x3031, 0x3032, 0x3033, 0x3034, 0x3035, 0x3036, 0x3037, 0x3038,
0x3039, 0x3130, 0x3131, 0x3132, 0x3133, 0x3134, 0x3135, 0x3136, 0x3137,
0x3138, 0x3139, 0x3230, 0x3231, 0x3232, 0x3233, 0x3234, 0x3235, 0x3236,
0x3237, 0x3238, 0x3239, 0x3330, 0x3331, 0x3332, 0x3333, 0x3334, 0x3335,
0x3336, 0x3337, 0x3338, 0x3339, 0x3430, 0x3431, 0x3432, 0x3433, 0x3434,
0x3435, 0x3436, 0x3437, 0x3438, 0x3439, 0x3530, 0x3531, 0x3532, 0x3533,
0x3534, 0x3535, 0x3536, 0x3537, 0x3538, 0x3539, 0x3630, 0x3631, 0x3632,
0x3633, 0x3634, 0x3635, 0x3636, 0x3637, 0x3638, 0x3639, 0x3730, 0x3731,
0x3732, 0x3733, 0x3734, 0x3735, 0x3736, 0x3737, 0x3738, 0x3739, 0x3830,
0x3831, 0x3832, 0x3833, 0x3834, 0x3835, 0x3836, 0x3837, 0x3838, 0x3839,
0x3930, 0x3931, 0x3932, 0x3933, 0x3934, 0x3935, 0x3936, 0x3937, 0x3938,
0x3939 };To optimize the search for the size we must calculate the min and max values of the corresponding string lengths and bit widths. Below is a table of 2^N of the ranges where the string length differs by one and where N is an integer in the range [1, 32]. For grouping purposes, there is no length 0 through 1 group so groups start at length 1-2, 2-3,..., 9-10 for a total of 10 groups.
| ##bits | min | max | mid | ##bits | min | max | mid |
|---|---|---|---|---|---|---|---|
| 1 | 0.00E+00 | 1.00E+00 | 0.00E+00 | 17 | 6.55E+04 | 1.31E+05 | |
| 2 | 2.00E+00 | 3.00E+00 | 2.00E+00 | 18 | 1.31E+05 | 2.62E+05 | 1.97E+05 |
| 3 | 4.00E+00 | 7.00E+00 | 5.00E+00 | 19 | 2.62E+05 | 5.24E+05 | 3.93E+05 |
| 4 | 8.00E+00 | 1.50E+01 | 20 | 5.24E+05 | 1.05E+06 | ||
| 5 | 1.60E+01 | 3.10E+01 | 2.30E+01 | 21 | 1.05E+06 | 2.10E+06 | 1.57E+06 |
| 6 | 3.20E+01 | 6.30E+01 | 4.70E+01 | 22 | 2.10E+06 | 4.19E+06 | 3.15E+06 |
| 7 | 6.40E+01 | 1.27E+02 | 23 | 4.19E+06 | 8.39E+06 | 6.29E+06 | |
| 8 | 1.28E+02 | 2.55E+02 | 1.91E+02 | 24 | 8.39E+06 | 1.68E+07 | |
| 9 | 2.56E+02 | 5.11E+02 | 3.83E+02 | 25 | 1.68E+07 | 3.36E+07 | 2.52E+07 |
| 10 | 5.12E+02 | 1.02E+03 | 26 | 3.36E+07 | 6.71E+07 | 5.03E+07 | |
| 11 | 1.02E+03 | 2.05E+03 | 1.54E+03 | 27 | 6.71E+07 | 1.34E+08 | |
| 12 | 2.05E+03 | 4.10E+03 | 3.07E+03 | 28 | 1.34E+08 | 2.68E+08 | 2.01E+08 |
| 13 | 4.10E+03 | 8.19E+03 | 6.14E+03 | 29 | 2.68E+08 | 5.37E+08 | 4.03E+08 |
| 14 | 8.19E+03 | 1.64E+04 | 30 | 5.37E+08 | 1.07E+09 | ||
| 15 | 1.64E+04 | 3.28E+04 | 2.46E+04 | 31 | 1.07E+09 | 2.15E+09 | 1.61E+09 |
| 16 | 3.28E+04 | 6.55E+04 | 4.92E+04 | 32 | 2.15E+09 | 4.29E+09 | 3.22E+09 |
One very important observation is that most of the string lengths are clustered into groups of 3 or 4. Another observation is that on the edge cases where the length changes by one decimal, the MSD of that value will always be a 1. We can use this property to more quickly convert the MSD when you are searching for the converted number string length.
In order to convert the integer, you need to search for the length. Numbers length 1 and 2 may quickly be converted without any division. For these numbers, the overhead of the function call is a much higher ratio so it really speeds up the algorithm to have those lengths be the fastest paths. For large numbers with lots of division instructions, it doesn't matter if there is an extra nested if statement so the largest numbers need to be the highest nested level. For these reasons sizes where searched for in groups of 3 digits in the root, 3 digits in the first nested if level, and 2 digits in the next level for lengths 7 and 8 and two more digits in the last nested level (@note this will change to groups of 3, 3 and 4.
There are two fast MSD conversion techniques used in the Puff ItoS Algorithm. The first MSD conversion occurs when the MSD of the bit ranges from Section 2.3.a is a 1. This process is further optimized by choosing the path with the smallest range as the nested if statement.
The second conversion optimization is to convert the values in pairs of 4 or less and to use 16-bit division, multiplication, and subtraction rather than slot 32-bit modulo and division. Conversion of groups of 4 digits starts by dividing the four decimal pair by 100 to calculate the two MSD. This value is then multiplied by 100 and subtracted from the original value to make the 2 least significant digits. To split the number into groups of four the same manual modulo math is used by dividing the number by 10,000 then performing the manual modulo 100 on both groups.
Dividing into pairs of four allows for about 1/3 of the division instructions to be skipped. The algorithm works fastest for numbers with 8 digits and works flawlessly with any number of bits. For strings length 5 this is an edge case where the same number of division instructions are used in as are used in the Mod100 Algorithm.
template <typename Char = char>
inline Char* Print8Decimals(Char* cursor, uint32_t value_ui4,
const uint16_t* lut) {
PRINT("\n Printing 8 decimals:"); // Example value is 12345678
PRINT(value_ui4);
uint16_t pow_10_ui2 = 10000, digits6and5 = (uint16_t)(value_ui4 / pow_10_ui2),
digits2and1 = value_ui4 - pow_10_ui2 * digits6and5;
pow_10_ui2 = 100;
uint16_t digits8and7 = digits6and5 / pow_10_ui2,
digits4and3 = digits2and1 / pow_10_ui2;
digits6and5 -= pow_10_ui2 * digits8and7;
digits2and1 -= pow_10_ui2 * digits4and3;
PrintCharPair(cursor, lut[digits8and7]);
PrintCharPair(cursor + 2, lut[digits6and5]);
PrintCharPair(cursor + 4, lut[digits4and3]);
PrintCharPair(cursor + 6, lut[digits2and1]);
PRINT_PRINTED; //< This is a macro defined below.
return cursor + 8;
}Lets contrast that with an unrolled modulo 100 loop and count the division and modulo instructions.
uint32_t value = 12345678;
char buffer[9];
uint16_t* buffer_ui2 = reinterpret_cast<uint16_t*>(buffer);
buffer_ui2[6] = kDigits00To99[value % 100];
value /= 100;
buffer_ui2[4] = kDigits00To99[value % 100];
value /= 100;
buffer_ui2[2] = kDigits00To99[value % 100];
buffer_ui2[0] = kDigits00To99[value / 100];
buffer[8] = 0;The first thing to notice is that the final converted decimal pair does not require a modulo. The unrolled modulo loop can count is 3 modulo instructions and 3 divisions. In the Puff ItoS algorithm, we count a grand total of 3, yes count them 3, division instructions. We essentially are only performing the three modulo instructions. Now lets contrast this to not using the groupings of 8:
char buffer[9];
uint16_t* buffer_ui2 = reinterpret_cast<uint16_t*>(buffer);
uint32_t value = 12345678,
msds; //< Most significant decimals.
buffer_ui2[6] = kDigits00To99[digits];
hundreds = value / 100;
msds = value - 100 * hundreds;
digits = value - msds;
value -= msds;
buffer_ui2[4] = kDigits00To99[digits];
buffer_ui2[6] = kDigits00To99[digits];
hundreds = value / 100;
msds = value - 100 * hundreds;
digits = value - msds;
value -= msds;
buffer_ui2[2] = kDigits00To99[digits];
buffer_ui2[0] = kDigits00To99[value / 100];One can easily count up the number of division instructions and sure enough, there are four division instructions compared to the 3 division instructions in the Puff algorithm.
In order to eliminate the kDigits00To99 LUT, all one must do is perform manual modulo 10 on the two-digit values.
template<typename Char>
inline Char* PrintTwoDigits (Char* cursor, uintptr_t value) {
Char msd = ((Char)value) / 10,
lsd = ((Char)value) - msd * 10;
*cursor++ = '0' + msd;
*cursor++ = '0' + lsd;
return cursor;
}Below is the Puff ItoS Algorithm with the debug information included so you can watch the algorithm at work. The algorithm is not presented in header-only format because it contains static data that would get duplicated in an executable if compiled into a precompiled library. The file organization is engineered for rapid compilation by hiding through the use of a C Application Binary Interface (ABI) with hidden C++ template implementation. This provides faster compilation time than the C equivalent while providing an easier to understand algorithm.
There is a compelling argument for the use of C++ over C for this circumstance. The algorithm below combines all of the code needed both print and scan integers and floating-point numbers in one algorithm. The use of goto statements is also a Flywheel Design Pattern because it reuses the same section of code.
/* Kabuki Toolkit @version 0.x
@link https://github.com/kabuki-starship/kabuki-toolkit.git
@file $kabuki-toolkit/kabuki/crabs/tbinary.h
@author Cale McCollough <[email protected]>
@license Copyright (C) 2018 Cale McCollough <calemccollough.github.io>;
All right reserved (R). Licensed under the Apache License, Version 2.0 (the
"License"); you may not use this file except in compliance with the License.
You may obtain a copy of the License at www.apache.org/licenses/LICENSE-2.0.
Unless required by applicable law or agreed to in writing, software distributed
under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR
CONDITIONS OF ANY KIND, either express or implied. See the License for the
specific language governing permissions and limitations under the License. */
#include <cstdint>
#define SEAM 1
#if SEAM == 0
#include <cstdint>
#include <cstdio>
#include <cstdargs>
#include <cstring>
namespace _ {
template <typename Char>
void PrintString(const Char* string) {
ASSERT(string);
Char c = *string;
while (c) {
Print(c);
c = *(++string);
}
}
template <typename Char>
intptr_t PrintAndCount(const Char* string) {
ASSERT(string);
int print_count = 0;
Char c = *string;
while (c) {
Print(c);
++print_count;
c = *(++string);
}
return print_count;
}
template <typename Char>
Char* PuffItoSBegin(Char* cursor = nullptr) {
static Char* buffer_begin = 0;
if (cursor) {
buffer_begin = cursor;
return cursor;
}
return buffer_begin;
}
template <typename Char>
void PrintPrinted(Char* cursor) {
Print("\n Printed \"");
intptr_t print_count = PrintAndCount<Char>(PuffItoSBegin<Char>());
Print(':');
Print(print_count);
}
inline void Print (char c) {
putchar (c);
}
inline void Print (const char* string) {
printf (string);
}
#define PRINT(item) Print(item)
#define PRINTF(format, ...) printf(format, __VA_ARGS__)
#define PRINT_PRINTED PrintPrinted<Char>(PuffItoSBegin<Char>())
#define BEGIN_ITOS_ALGORITHM \
static const char* ui_format = sizeof(UI) == 8 ? FORMAT_UI8 : "%u"; \
PuffItoSBegin<Char>(cursor); \
for (int32_t i = 0; i < 10; ++i) *(cursor + i) = 'x'; \
*(cursor + 21) = 0; \
enum { kSize = 256 }; \
char buffer[kSize]; \
sprintf_s(buffer, kSize, ui_format, value); \
printf(" Expecting %s:%i ", buffer, StringLength<Char>(buffer))
#else
#define PRINT(item)
#define PRINTF(x, ...)
#define PRINT_PRINTED ;
#define BEGIN_ITOS_ALGORITHM
#endif
namespace _ {
/* Prints two chars to the console.
@warning This function DOES NOT do any error checking! */
template <typename Char = char>
inline Char* PrintNil(Char* cursor) {
*cursor = 0;
return cursor;
}
/* Prints a two decimals to the buffer.
If the SEAM == SEAM_0_0_0 (1), then this function will print debug data.
@warning This function DOES NOT do any error checking! */
template <typename Char = char>
inline Char* Print2Decimals(Char* buffer, uint16_t decimal_pair) {
enum { kSizeBits = sizeof(Char) * 8 };
buffer[0] = (Char)(decimal_pair >> 8);
char c = (char)decimal_pair;
buffer[1] = (Char)(c);
PRINT_PRINTED;
return buffer;
}
inline char* PrintCharPair(char* buffer, uint16_t value) {
#if ALIGN_MEMORY
buffer[0] = (char)(value >> 8);
buffer[1] = (char)(value);
#else
*((uint16_t*)buffer) = value;
#endif
using Char = char;
PRINT_PRINTED;
return buffer;
}
inline char16_t* PrintCharPair(char16_t* cursor, uint16_t decimal_pair) {
return Print2Decimals<char16_t>(cursor, decimal_pair);
}
inline char32_t* PrintCharPair(char32_t* cursor, uint16_t decimal_pair) {
return Print2Decimals<char32_t>(cursor, decimal_pair);
}
template <typename Char = char>
inline Char* Print8Decimals(Char* cursor, uint32_t value_ui4,
const uint16_t* lut);
template <typename Char = char>
inline void Print8or16Decimals(Char* cursor, uint32_t lsd, const uint16_t* lut,
uint32_t middle_sd, uint32_t delta) {
if (delta == 8) {
PRINTF("\n Printing less than 15 decimals:");
Print8Decimals<Char>(cursor, lsd, lut);
} else {
PRINTF("\n Printing more than 16 decimals:");
Print8Decimals<Char>(cursor, middle_sd, lut);
Print8Decimals<Char>(cursor + 8, lsd, lut);
}
}
/* Utility function for casting templated 32-bit UI. */
inline uint32_t ValueUI4(uint32_t value) { return value; }
/* Utility function for casting templated 32-bit UI. */
inline uint32_t ValueUI4(uint64_t value) { return (uint32_t)value; }
/* Prints the give value to the given buffer as a Unicode string.
@return Nil upon buffer overflow and a pointer to the nil-term Char upon
success.
@param cursor The beginning of the buffer.
@param end The end address of the buffer. */
template <typename UI = uint64_t, typename Char = char>
Char* PrintUnsigned(Char* cursor, Char* end, UI value) {
BEGIN_ITOS_ALGORITHM;
if (!cursor || cursor >= end) return nullptr;
Char* nil_ptr;
uint16_t pow_10_ui2;
uint32_t pow_10_ui4, delta = 0;
const uint16_t* lut = PuffDigitsLut();
// The best way to understand how the numbers are getting converted is that
// numbers get broken up into up to 8 pairs of 100, in each pair of 10000
// there will be a Most Significant Decimal (MSD) pair and a Least
// Significant Decimal (LSD) pair. The digits2and1 and digits6and5 will
// always be the LSD and digits4and3 and digits8and7 will always be the MSD.
if (value < 10) {
PRINT("\n Range:[0, 9] length:1 ");
Print1:
nil_ptr = cursor + delta + 1;
if (nil_ptr >= end) return nullptr;
PrintDecimal<Char>(cursor, (Char)value);
return PrintNil<Char>(cursor + delta + 1);
} else if (value < 100) {
Print2:
PRINT("\n Range:[10, 99] length:2 ");
nil_ptr = cursor + delta + 2;
if (cursor + delta + 2 >= end) return nullptr;
PrintCharPair(cursor, lut[value]);
return PrintNil<Char>(cursor + delta + 2);
} else {
if ((value >> 10) == 0) {
pow_10_ui2 = 1000;
if (value >= pow_10_ui2) {
Print4A:
PRINT("\n Range:[1000, 1023] length:4");
nil_ptr = cursor + delta + 4;
if (nil_ptr >= end) return nullptr;
uint16_t digits2and1 = (uint16_t)(value - pow_10_ui2);
#if CPU_ENDIAN == LITTLE_ENDIAN
cursor[0] = '1';
cursor[1] = '0';
#else
cursor[0] = '0';
cursor[1] = '1';
#endif
PrintCharPair(cursor + 2, lut[digits2and1]);
return PrintNil<Char>(nil_ptr);
}
Print3:
PRINT("\n Range:[100, 999] length:3");
nil_ptr = cursor + delta + 3;
if (nil_ptr >= end) return nullptr;
uint16_t digits2and1 = (uint16_t)value, pow_10_ui2 = 100;
Char digit = (Char)(digits2and1 / pow_10_ui2);
digits2and1 -= digit * pow_10_ui2;
PrintDecimal<Char>(cursor, digit);
PrintCharPair(cursor + 1, lut[digits2and1]);
return PrintNil<Char>(nil_ptr);
} else if ((value >> 14) == 0) {
pow_10_ui2 = 10000;
if (value >= pow_10_ui2) {
Print5A:
PRINT("\n Range:[10000, 16383] length:5");
nil_ptr = cursor + delta + 5;
if (nil_ptr >= end) return nullptr;
cursor = PrintChar<Char>(cursor, '1');
value -= pow_10_ui2;
} else {
Print4:
PRINT("\n Range:[1024, 9999] length:4");
nil_ptr = cursor + delta + 4;
if (nil_ptr >= end) return nullptr;
PrintNil<Char>(nil_ptr);
}
pow_10_ui2 = 100;
uint16_t digits2and1 = (uint16_t)value,
digits4and3 = digits2and1 / pow_10_ui2;
digits2and1 -= digits4and3 * pow_10_ui2;
PrintCharPair(cursor, lut[digits4and3]);
PrintCharPair(cursor + 2, lut[digits2and1]);
return PrintNil<Char>(nil_ptr);
} else if ((value >> 17) == 0) {
if (value >= 100000) {
Print6A:
PRINT("\n Range:[65536, 131071] length:6");
goto Print6;
}
Print5:
PRINT("\n Range:[10000, 65535] length:5");
nil_ptr = cursor + delta + 5;
if (nil_ptr >= end) return nullptr;
uint32_t value_ui4 = ValueUI4(value);
pow_10_ui2 = 10000;
Char digit6 = (uint8_t)(value_ui4 / pow_10_ui2);
value_ui4 -= pow_10_ui2 * digit6;
cursor = PrintChar<Char>(cursor, '0' + digit6);
pow_10_ui2 = 100;
uint16_t digits4and3 = ((uint16_t)value_ui4) / pow_10_ui2,
digits2and1 = (uint16_t)(value_ui4 - digits4and3 * pow_10_ui2);
PrintCharPair(cursor, lut[digits4and3]);
PrintCharPair(cursor + 2, lut[digits2and1]);
return PrintNil<Char>(nil_ptr);
} else if ((value >> 20) == 0) {
pow_10_ui4 = 1000000;
if (value >= pow_10_ui4) {
Print7A:
PRINT("\n Range:[100000, 1048575] length:7");
nil_ptr = cursor + delta + 7;
if (nil_ptr >= end) return nullptr;
cursor = PrintChar(cursor, '1');
value -= pow_10_ui4;
} else {
Print6:
PRINT("\n Range:[131072, 999999] length:6");
nil_ptr = cursor + delta + 6;
if (nil_ptr >= end) return nullptr;
PrintNil<Char>(nil_ptr);
}
uint32_t value_ui4 = (uint32_t)value;
pow_10_ui2 = 10000;
uint16_t digits6and5 = (uint16_t)(value_ui4 / pow_10_ui2),
digits2and1 = value_ui4 - pow_10_ui2 * digits6and5;
pow_10_ui2 = 100;
uint16_t digits8and7 = digits6and5 / pow_10_ui2,
digits4and3 = digits2and1 / pow_10_ui2;
digits6and5 -= pow_10_ui2 * digits8and7;
digits2and1 -= pow_10_ui2 * digits4and3;
PrintCharPair(cursor, lut[digits6and5]);
PrintCharPair(cursor + 2, lut[digits4and3]);
PrintCharPair(cursor + 4, lut[digits2and1]);
return nil_ptr;
} else if ((value >> 24) == 0) {
pow_10_ui4 = 10000000; //< 10^7
if (value >= pow_10_ui4) {
PRINT("\n Range:[10000000, 16777216] length:8");
return Print8Decimals<Char>(cursor, ValueUI4(value), lut);
}
Print7:
PRINT("\n Range:[1048576, 9999999] length:7");
Print7B:
nil_ptr = cursor + delta + 7;
if (nil_ptr >= end) return nullptr;
uint16_t pow_10_ui2 = 10000;
uint32_t value_ui4 = ValueUI4(value);
uint16_t digits6and5 = value_ui4 / pow_10_ui2,
digits2and1 = value_ui4 - pow_10_ui2 * digits6and5;
pow_10_ui2 = 100;
uint16_t digit7 = digits6and5 / pow_10_ui2,
digits4and3 = digits2and1 / pow_10_ui2;
digits6and5 -= pow_10_ui2 * digit7;
digits2and1 -= pow_10_ui2 * digits4and3;
PrintDecimal(cursor, (Char)(digit7));
PrintCharPair(cursor + 1, lut[digits6and5]);
PrintCharPair(cursor + 3, lut[digits4and3]);
PrintCharPair(cursor + 5, lut[digits2and1]);
return PrintNil<Char>(nil_ptr);
} else {
uint32_t comparator = 100000000; // 10^8
UI msd = (value >= (~(uint32_t)0)) ? value / comparator
: ValueUI4(value) / comparator;
uint32_t lsd = (uint32_t)(value - comparator * msd), middle_sd;
if (msd >= comparator) {
delta = 16;
value = msd / comparator;
middle_sd = ValueUI4(msd - value * comparator);
PRINT(value);
PRINT('_');
PRINT(middle_sd);
PRINT('_');
PRINT(lsd);
} else {
value = msd;
middle_sd = 0;
delta = 8;
PRINT(value);
PRINT('_');
PRINT(lsd);
}
if (value < 10) {
Print8or16Decimals<Char>(cursor + 1, lsd, lut, middle_sd, delta);
goto Print1;
} else if (value < 100) {
Print8or16Decimals<Char>(cursor + 2, lsd, lut, middle_sd, delta);
goto Print2;
}
if ((value >> 10) == 0) {
pow_10_ui2 = 1000;
if (value >= pow_10_ui2) {
Print8or16Decimals<Char>(cursor + 4, lsd, lut, middle_sd, delta);
goto Print4A;
}
Print8or16Decimals<Char>(cursor + 3, lsd, lut, middle_sd, delta);
goto Print3;
} else if ((value >> 13) == 0) {
pow_10_ui2 = 10000;
if (value >= pow_10_ui2) {
Print8or16Decimals<Char>(cursor + 5, lsd, lut, middle_sd, delta);
goto Print5A;
}
Print8or16Decimals<Char>(cursor + 4, lsd, lut, middle_sd, delta);
goto Print4;
} else if ((value >> 17) == 0) {
pow_10_ui4 = 100000;
if (value >= pow_10_ui4) {
Print8or16Decimals<Char>(cursor + 6, lsd, lut, middle_sd, delta);
goto Print6A;
}
Print8or16Decimals<Char>(cursor + 5, lsd, lut, middle_sd, delta);
goto Print5;
} else if ((value >> 20) == 0) {
pow_10_ui4 = 1000000;
if (value >= pow_10_ui4) {
Print8or16Decimals<Char>(cursor + 7, lsd, lut, middle_sd, delta);
goto Print7A;
}
Print8or16Decimals<Char>(cursor + 6, lsd, lut, middle_sd, delta);
goto Print6;
} else {
comparator = 10000000;
if (value >= comparator) {
PRINTF("\n Printing 16 decimals:");
PRINT(value);
PRINT('_');
PRINT(lsd);
Print8Decimals<Char>(cursor, ValueUI4(value), lut);
Print8Decimals<Char>(cursor + 8, lsd, lut);
return PrintNil<Char>(cursor + 16);
}
Print8or16Decimals<Char>(cursor + 7, lsd, lut, middle_sd, delta);
goto Print7;
}
}
}
return nullptr; //< Unreachable.
}
} //< namespace _
#undef PRINT
#undef PRINTF
#undef PRINT_PRINTED
#undef BEGIN_ITOS_ALGORITHM
#endifThe benchmarks consist of a time delta for each number of bits 1-32 and three sets of data. Benchmark excludes sprintf because it takes so long it squishes the benchmark too much to see the fastest algorithms.
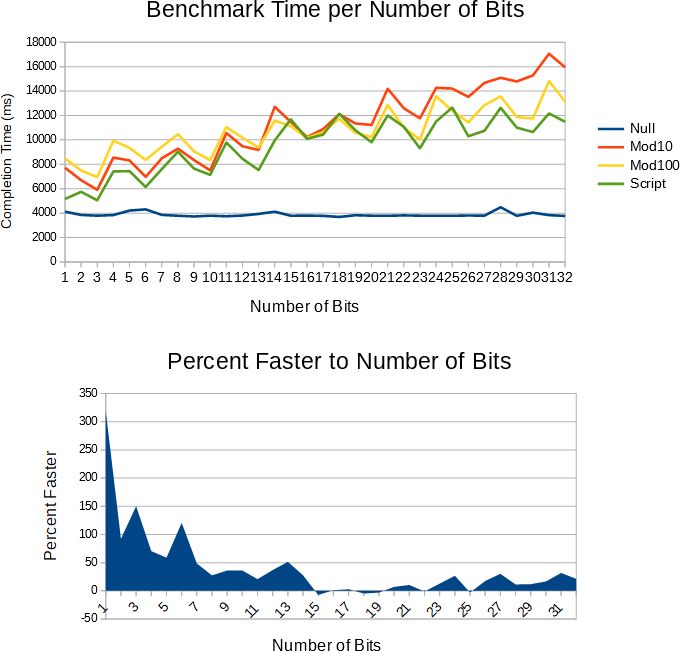
For detailed benchmark values, please visit https://goo.gl/xaj2si. For the benchmark code, please visit https://goo.gl/DBAooi and for benchmark methodology please read our article Benchmarking Software in C++ at https://goo.gl/i7NFJf.
The Grisu algorithm was written by Florian Loitsch[A]. It was originally taken by from Milo Yip[B]. The primary increase in performance comes from performing manual modulo rather than mod 10 div 10. There is some speed up from applying the Puff size search technique, but it is minimal setup compared to the division loops.
/* A decimal number in floating-point format. */
template <typename Char>
Char* TPrint3(Char* buffer, Char* end, Char a, Char b, Char c) {
if (!buffer || buffer + 3 >= end) return nullptr;
*buffer++ = a;
*buffer++ = b;
*buffer++ = c;
}
/* A decimal number in floating-point format. */
template <typename Float = DBL, typename UI = UI8>
class TBinary {
public:
static int Foo() { return 1; }
enum {
kSize = sizeof(Float),
kSizeBits = kSize * 8,
kMSbIndex = kSizeBits - 1,
kStringLengthMax = 24,
kExponentSizeBits =
(sizeof(Float) == 2)
? 5
: (sizeof(Float) == 4) ? 8 : (sizeof(Float) == 8) ? 11 : 15,
kCoefficientSize = kSizeBits - kExponentSizeBits - 1,
kMantissaSize = kSizeBits - kExponentSizeBits - 2,
kExponentMaskUnshifted = (~((UI)0)) >> (kSizeBits - kExponentSizeBits),
kExponentBias = kExponentMaskUnshifted + kCoefficientSize,
kExponentMin = -kExponentBias,
};
// Constructs an uninitialized floating-point number.
TBinary() {}
inline static UI Coefficient(UI decimal) {
return (decimal << (kExponentSizeBits + 1)) >> (kExponentSizeBits + 1);
}
// Converts a Float to a TBinary
TBinary(Float binary) {
UI ui = *reinterpret_cast<UI*>(&binary);
UI4 biased_e = (UI4)(ui << 1); //< Get rid of sign bit.
// Get rid of the integral portion.
biased_e = biased_e >> (kSizeBits - kExponentSizeBits);
// Get rid of the sign and exponent.
UI8 coefficient = Coefficient(binary);
if (biased_e != 0) {
f = coefficient + (((UI)1) << kExponentSizeBits);
e = biased_e - kExponentBias;
} else {
f = coefficient;
e = kExponentMin + 1;
}
}
TBinary(UI f, SI4 e) : f(f), e(e) {}
TBinary(const TBinary a, const TBinary b) {}
inline static UI Exponent(UI decimal) {
return (decimal << (kExponentSizeBits + 1)) >> (kExponentSizeBits + 1);
}
template <typename Char = char>
static Char* Print(Char* buffer, Char* end, Float value) {
// Not handling NaN and inf
if (IsNaN(value)) {
if (end - buffer < 4) return nullptr;
buffer[0] = 'N';
buffer[1] = 'a';
buffer[2] = 'N';
buffer[3] = 0;
return buffer + 4;
}
if (IsInfinite(value)) {
if (end - buffer < 4) return nullptr;
UI f = *reinterpret_cast<UI*>(&value);
buffer[0] = (f >> (sizeof(UI) * 8 - 1)) ? '-' : '+';
buffer[1] = 'i';
buffer[2] = 'n';
buffer[3] = 'f';
buffer[4] = 0;
return buffer + 5;
}
if (value == 0) {
return TPrint3<Char>(buffer, end, (Char)'0', (Char)'.', (Char)'0');
}
if (value < 0) {
*buffer++ = '-';
value = -value;
}
SI4 k;
Char* cursor = TPrint<Char>(buffer, end, value, k);
if (!cursor) return cursor;
return Standardize<Char>(buffer, end, cursor - buffer, k);
}
template <typename UI = UIW>
static inline UI NaNUnsigned() {
UI nan = 0;
return ~nan;
}
template <typename SI, typename UI>
static inline SI TNaNSigned() {
UI nan = 1;
return (SI)(nan << (sizeof(UI) * 8 - 1));
}
static TBinary IEEE754Pow10(SI4 e, SI4& k) {
// SI4 k = static_cast<SI4>(ceil((-61 - e) *
// 0.30102999566398114))
// + 374; dk must be positive to perform ceiling function on positive
// values.
Float dk = (-61 - e) * 0.30102999566398114 + 347;
k = static_cast<SI4>(dk);
if (k != dk) ++k;
UI4 index = static_cast<UI4>((k >> 3) + 1);
k = -(-348 + static_cast<SI4>(index << 3));
// decimal exponent no need lookup table.
ASSERT(index < 87);
// Save exponents pointer and offset to avoid creating base pointer again.
return TBinary(BinaryLUTF()[index], BinaryLUTE()[index]);
}
private:
UI f;
SI4 e;
static inline void Multiply(TBinary& result, TBinary& a, TBinary& b) {}
template <typename Char>
static Char* Print(Char* buffer, Char* end, Float value, SI4& k) {
TBinary v(value);
TBinary lower_estimate, upper_estimate;
v.NormalizedBoundaries(lower_estimate, upper_estimate);
TBinary c_mk = IEEE754Pow10(upper_estimate.e, k);
TBinary W(v.NormalizeBoundary(), c_mk);
TBinary w_plus(upper_estimate, c_mk), w_minus(lower_estimate, c_mk);
w_minus.f++;
w_plus.f--;
return DigitGen<Char>(buffer, end, W, w_plus, w_plus.f - w_minus.f, k);
}
TBinary NormalizeBoundary() const {
// int msba = MSbAsserted(0);
#if defined(_MSC_VER) && defined(_M_AMD64)
unsigned long index; //< This is Microsoft's fault.
_BitScanReverse64(&index, f);
return TBinary(f << (kMSbIndex - index), e - (kMSbIndex - index));
#else
TBinary res = *this;
UI kDpHiddenBit = ((UI)1) << kMantissaSize; // 0x0010000000000000;
while (!(res.f & (kDpHiddenBit << 1))) {
res.f <<= 1;
--res.e;
}
res.f <<= (kDiySignificandSize - kCoefficientSize - 2);
res.e = res.e - (kDiySignificandSize - kCoefficientSize - 2);
return res;
#endif
}
// static const UI8 kDpExponentMask = 0x7FF0000000000000,
// kDpSignificandMask = 0x000FFFFFFFFFFFFF,
// Normalizes the boundaries.
void NormalizedBoundaries(TBinary& m_minus, TBinary& m_plus) const {
UI l_f, //< Local copy of f.
l_e; //< Local copy of e.
TBinary pl = TBinary((l_f << 1) + 1, ((SI4)l_e) - 1).NormalizeBoundary();
const UI8 kHiddenBit = ((UI8)1) << kMantissaSize; //< 0x0010000000000000
TBinary mi = (f == kHiddenBit) ? TBinary((l_f << 2) - 1, e - 2)
: TBinary((l_f << 1) - 1, e - 1);
mi.f <<= mi.e - pl.e;
mi.e = pl.e;
m_plus = pl;
m_minus = mi;
}
// Rounds the Grisu estimation closer to the inside of the squeeze.
template <typename Char>
static void Round(Char& lsd, UI delta, UI rest, UI ten_kappa, UI wp_w) {
while (rest < wp_w && (delta - rest) >= ten_kappa &&
(rest + ten_kappa < wp_w || /// closer
(wp_w - rest) > (rest + ten_kappa - wp_w))) {
--lsd;
rest += ten_kappa;
}
}
// Prints the integer portion of the floating-point number.
//@return Nil upon failure or a pointer to the nil-term Char upon success.
template <typename Char>
static Char* DigitGen(Char* cursor, Char* end, const TBinary& w,
const TBinary& m_plus, UI8 delta, SI4& k) {
TBinary one(((UI8)1) << -m_plus.e, m_plus.e), wp_w = m_plus - w;
UI4 d, pow_10, p_1 = static_cast<UI4>(m_plus.f >> -one.e);
UI8 p_2 = m_plus.f & (one.f - 1);
int kappa;
if (p_1 < (pow_10 = 10)) {
kappa = 1;
} else if (p_1 < (pow_10 = 100)) {
kappa = 2;
} else {
if ((p_1 >> 10) == 0) {
kappa = 3;
pow_10 = 1000;
} else if (!(p_1 >> 13)) {
kappa = 4;
pow_10 = 10000;
} else if (!(p_1 >> 17)) {
kappa = 5;
pow_10 = 100000;
} else if (!(p_1 >> 20)) {
kappa = 6;
pow_10 = 1000000;
} else if (!(p_1 >> 24)) {
kappa = 7;
pow_10 = 10000000;
} else if (!(p_1 >> 27)) {
kappa = 8;
pow_10 = 100000000;
} else if (!(p_1 >> 30)) {
kappa = 9;
pow_10 = 1000000000;
} else {
kappa = 10;
pow_10 = 10000000000;
}
if (p_1 >= pow_10) {
++kappa;
pow_10 *= 10;
}
}
while (kappa > 0) {
UI4 d;
d = p_1 / pow_10;
p_1 -= d * pow_10;
if (cursor >= end) return nullptr;
if (d) cursor = TPrintDecimal<Char>(cursor, d);
--kappa;
UI tmp = (static_cast<UI8>(p_1) << -one.e) + p_2;
if (tmp <= delta) {
k += kappa;
Round(delta, tmp, IEEE754Pow10(kappa) << -one.e, wp_w.f);
return;
}
}
for (;;) { // kappa = 0
p_2 *= 10;
delta *= 10;
char d = static_cast<char>(p_2 >> -one.e);
if (cursor >= end) return nullptr;
if (d) *cursor++ = '0' + d;
p_2 &= one.f - 1;
--kappa;
if (p_2 < delta) {
k += kappa;
Round(delta, p_2, one.f, wp_w.f * IEEE754Pow10(-kappa));
return;
}
}
// Load integer pow_10 from the i-cache.
switch (kappa) {
case 1:
d = p_1;
p_1 = 0;
break;
case 2:
pow_10 = 10;
break;
case 3:
pow_10 = 100;
break;
case 4:
pow_10 = 1000;
break;
case 5:
pow_10 = 10000;
break;
case 6:
pow_10 = 100000;
break;
case 7:
pow_10 = 1000000;
break;
case 8:
pow_10 = 10000000;
break;
case 9:
pow_10 = 100000000;
break;
case 10:
pow_10 = 1000000000;
break;
}
}
template <typename Char = char>
static Char* Standardize(Char* buffer, Char* end, SIW length, SI4 k) {
const SIW kk = length + k; // 10^(kk-1) <= v < 10^kk
Char* nil_term_char;
if (length <= kk && kk <= 21) { // 1234e7 -> 12340000000
for (SIW i = length; i < kk; i++) buffer[i] = '0';
buffer[kk] = '.';
buffer[kk + 1] = '0';
nil_term_char = &buffer[kk + 2];
*nil_term_char = '\0';
return nil_term_char;
} else if (0 < kk && kk <= 21) { // 1234e-2 -> 12.34
SocketShiftUp(&buffer[kk + 1], LastByte(&buffer[kk]), length - kk);
buffer[kk] = '.';
nil_term_char = &buffer[length + 1];
*nil_term_char = '\0';
return nil_term_char;
} else if (-6 < kk && kk <= 0) { // 1234e-6 -> 0.001234
const SIW offset = 2 - kk;
SocketShiftUp(&buffer[offset], LastByte(&buffer[0]), length);
buffer[0] = '0';
buffer[1] = '.';
for (SIW i = 2; i < offset; i++) buffer[i] = '0';
nil_term_char = &buffer[length + offset];
*nil_term_char = 0;
return nil_term_char;
} else if (length == 1) {
// 1e30
buffer[1] = 'e';
return TPrintSigned<SIW, Char>(buffer + 2, end, kk - 1);
}
// else 1234e30 -> 1.234e33
SocketShiftUp(&buffer[2], LastByte(&buffer[1]), length - 1);
*(++buffer)++ = '.';
*buffer++ = 'e';
return TPrintSigned<SIW, Char>(buffer + length + 2, end, kk - 1);
}
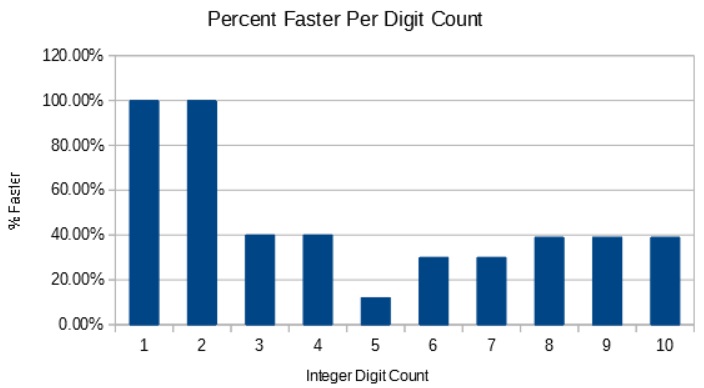
};The Puff Algorithm is a lot faster than the Modulo 10 and Modulo 100 techniques; on average about twice as fast for numbers less than 5 digits, a respectable 12% faster for 5 digits, and back up to about 30% to 39% faster for more than 6 digits. The Mod10 algorithm is faster than the Mod100 for 4 or fewer digits but the Modulo 100 performs better for large numbers; the Puff ItoS Algorithm, however, has the useful property that it outperforms both algorithms for both small and large numbers and when averaged out is still faster for integers strings of length 5. This performance though is entirely dependent on the range used in practice. The benchmarks per bit count and decimal count reveal different characteristics.
The raw benchmark of integers with 8 digits (i.e. the fastest case) is 39% tested in isolation without size search). When tested in isolation without any conditional statements the algorithm performs 40% faster, so with 8 digits only a small fraction of time is spent searching for the printed integer size. The number of bits benchmark is good at showing edge cases where the number of digits changes and may be more accurate, but in reality won't be because the maximum number will rarely be an even power of 2 so performance will be more similar to the next bit down. You have to take both the per-bit-count and per-digit-count benchmarks into account to get the full picture.
One fascinating point to note about the benchmark is where the Modulo 10 and Modulo 100 LUT algorithms converge from 14 bits to 18 bits. This range corresponds to max integer-to-string length of 5. This is where in the Puff ItoS algorithm there is a single MSD and a group of four digits to convert that adds up to the same number of divisions as the Mod100. The algorithms performances then diverge when the length greater than 5. This is why testing the algorithm per bit count is more revealing of the algorithm's performance as opposed to per number of digits.
The overall size of the Puff ItoS Algorithm is larger due to the special cases, making it not suitable for some embedded purposes. For embedded systems ROM size is often more important and the Modulo 10 technique may be preferred.
While printing numbers isn't a primary CPU task for most client-side apps it is a major CPU burden for many servers and it is very common to convert large JSON dictionaries and XML objects to text for serialization. Anyone who has had to sit there while a large JSON or XML object is being transceived knows how much time this can take, along with the fact that most of the numbers converted will be smaller. This savings for web servers and data centers could possibly be in millions of dollars in reduced power and the battery time saved on embedded systems can be significant. The Puff ItoS Algorithm has applications in the following fields:
- JSON/XML/OSC/Data serialization.
- Compilers.
- Database software.
- Web browsers.
- Internet protocols and routers.
- High-performance real-time systems.
- Battery powered systems.
- General purpose computing.
Future benchmarks will include SIMD optimizations and some minor tweaks to the algorithm and a mod 10 version of the algorithm. There is a small amount of jitter in the benchmark results and the next benchmark iteration will include a better benchmark convergence algorithm that exits after convergence to a specified error threshold.
The Puff Algorithm was invented for the Universal Text Formatter, which serves as the foundation for the F2 Foundational Framework and the Automaton Standard Code for Information Interchange (ASCII) Data Types, a replacement for the C++ std library suitable for embedded systems which is defined in the Serial Chinese Room, Interprocess, and Telemetry (SCRIPT) Specification, or Script for short sometimes called Script^2, and can be found online at https://github.com/kabuki-starship/script. Script^2 is the foundation of Kabuki Toolkit (KT), a modern cross-platform C/C++11 toolkit for making intelligent connected technologies, plugins, games, servers, firmware, and art. KT may be found online at https://github.com/kabuki-starship/kabuki-toolkit.
A. Printing Floating-Point Numbers Quickly and Accurately with Integers, Florian Loitsch 2011 Source: https://www.cs.tufts.edu/~nr/cs257/archive/florian-loitsch/printf.pdf B. dtoa-benchmark Milo Yip Source: https://github.com/miloyip/dtoa-benchmark