-
Notifications
You must be signed in to change notification settings - Fork 12
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Numerically inconsistent #47
Comments
|
It seems to be called from |
|
In https://github.com/cddlib/cddlib#numerical-problems they suggest playing with #define dd_almostzero 1.0E-6but I guess this would be quite difficult to change at the wrapper level compared to just recompiling |
|
You can compile it from source with a different constant and then copy the library in |
|
@blegat, is the following statement still true? You have upstreamed your changes, haven't you? Lines 10 to 13 in 4fbfa40
Also, if you are using any specific flags/options for the source compilation of Thank you very much! |
Indeed, this should be removed.
The full script is: |
|
I am still trying to get to the bottom of this issue. I cannot figure out what is happening... Below I compare the Julia output with the C output. Here is the set of vertices I'll compare: # Julia
vertices = [ -316.5 -109 -94.97
245 228 79
-160 132.3 109
-377.3 63.6 -99.1
-376.5 81.2 -93.4 ]And for the C version, I created this Call to testcdd1.c The Julia notebook throws the error here, when calling Lines 50 to 55 in c5c3633
Which is what I find very weird and cannot understand, since Any idea of what is going on? EditOK, my bad for not even questioning the output of |
|
The You need to transform it to a cone so you take the conic hull of the cartesian product of |
|
Ups... thanks! Indeed the output is now consistent with Julia's output: ➜ src git:(master) ✗ ./testcdd1
>> Input file: /home/henrique/Downloads/cddlib/examples-ext/test1.ext
input file /home/henrique/Downloads/cddlib/examples-ext/test1.ext is open
size = 5 x 4
Number Type = real
*Error: Numerical inconsistency is found. Use the GMP exact arithmetic. |
|
Not sure if we should close this issue or not yet. Otherwise, I ran into another "numerical inconsistent" issue: HalfSpace([-1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.0], 0.0)
HalfSpace([-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0], 0.0)
HalfSpace([-0.0, -26.0, -0.0, -0.0, -50.0, -35.0, -0.0, -25.0, -23.0, -26.0, -0.0, -0.0, -46.0, -23.0, -18.0], 0.0)
HalfSpace([-4.0, -42.0, -0.0, -29.0, -27.0, -5.0, -29.0, -25.0, -26.0, -24.0, -0.0, -26.0, -33.0, -0.0, -22.0], -37.0)
HalfSpace([-13.0, -0.0, -45.0, -10.0, -7.0, -0.0, -27.0, -19.0, -25.0, -11.0, -0.0, -8.0, -17.0, -6.0, 3.0], -47.0)
HalfSpace([-23.0, -0.0, -0.0, -0.0, -16.0, -44.0, -18.0, -3.0, -2.0, -0.0, -35.0, -45.0, -17.0, -5.0, -49.0], 0.0)
HalfSpace([-43.0, -0.0, -47.0, -34.0, -37.0, -0.0, -37.0, -47.0, -33.0, -35.0, -0.0, -46.0, -2.0, -27.0, 34.0], -47.0)
HalfSpace([-28.0, -11.0, -27.0, -25.0, -49.0, -0.0, -13.0, -0.0, -43.0, -11.0, -34.0, -23.0, -0.0, -33.0, 7.0], 0.0)
HalfSpace([-33.0, -0.0, -0.0, -38.0, -39.0, -0.0, -6.0, -47.0, -0.0, -0.0, -20.0, -0.0, -0.0, -19.0, -29.0], 0.0)
HalfSpace([-0.0, -0.0, -22.0, -0.0, -26.0, -0.0, -0.0, -37.0, -48.0, -21.0, -0.0, -38.0, -36.0, -40.0, 1.0], -9.0)
HalfSpace([-41.0, -5.0, -30.0, -14.0, -10.0, -0.0, -0.0, -31.0, -9.0, -11.0, -0.0, -49.0, -0.0, -36.0, -36.0], -19.0)
HalfSpace([-46.0, -4.0, -0.0, -31.0, -40.0, -36.0, -1.0, -22.0, -0.0, -21.0, -14.0, -0.0, -37.0, -34.0, 19.0], -1.0)
HalfSpace([-15.0, -0.0, -42.0, -3.0, -19.0, -38.0, -24.0, -17.0, -35.0, -41.0, -0.0, -0.0, -5.0, -8.0, -44.0], 0.0)
HalfSpace([-47.0, -0.0, -36.0, -0.0, -31.0, -0.0, -0.0, -6.0, -14.0, -8.0, -0.0, -20.0, -44.0, -0.0, -4.0], -35.0)
HalfSpace([-5.0, -0.0, -9.0, -23.0, -21.0, -19.0, -8.0, -8.0, -5.0, -2.0, -0.0, -22.0, -22.0, -43.0, 1.0], -5.0)
HalfSpace([-25.0, -0.0, -0.0, -11.0, -42.0, -0.0, -28.0, -46.0, -48.0, -37.0, -25.0, -38.0, -46.0, -19.0, -16.0], 0.0)
HalfSpace([-36.0, -0.0, -21.0, -0.0, -2.0, -0.0, -0.0, -41.0, -1.0, -49.0, -19.0, -0.0, -32.0, -23.0, -30.0], 0.0)Error: julia> Polyhedra.vrep(poly)
ERROR: Numerically inconsistent
Stacktrace:
[1] error(::String) at ./error.jl:33
[2] myerror(::Int32) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/error.jl:23
[3] dd_matrix2poly at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:53 [inlined]
[4] CDDLib.CDDPolyhedra{Float64,Float64}(::CDDLib.CDDInequalityMatrix{Float64,Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:68
[5] CDDLib.CDDPolyhedra(::CDDLib.CDDInequalityMatrix{Float64,Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedra.jl:83
[6] getpoly(::CDDLib.Polyhedron{Float64}, ::Bool) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:60
[7] getpoly at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:56 [inlined]
[8] getext(::CDDLib.Polyhedron{Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:51
[9] vrep(::CDDLib.Polyhedron{Float64}) at /home/mbesancon/.julia/packages/CDDLib/Y6ywi/src/polyhedron.jl:156
[10] top-level scope at REPL[106]:1The same polyhedron defined with |
|
For a more readable format, the polyhedron was created from the following JuMP model: cons[1] : 26 α[2] + 50 α[5] + 35 α[6] + 25 α[8] + 23 α[9] + 26 α[10] + 46 α[13] + 23 α[14] + 18 β ≥ 0.0
cons[2] : 4 α[1] + 42 α[2] + 29 α[4] + 27 α[5] + 5 α[6] + 29 α[7] + 25 α[8] + 26 α[9] + 24 α[10] + 26 α[12] + 33 α[13] + 22 β ≥ 37.0
cons[3] : 13 α[1] + 45 α[3] + 10 α[4] + 7 α[5] + 27 α[7] + 19 α[8] + 25 α[9] + 11 α[10] + 8 α[12] + 17 α[13] + 6 α[14] - 3 β ≥ 47.0
cons[4] : 23 α[1] + 16 α[5] + 44 α[6] + 18 α[7] + 3 α[8] + 2 α[9] + 35 α[11] + 45 α[12] + 17 α[13] + 5 α[14] + 49 β ≥ 0.0
cons[5] : 43 α[1] + 47 α[3] + 34 α[4] + 37 α[5] + 37 α[7] + 47 α[8] + 33 α[9] + 35 α[10] + 46 α[12] + 2 α[13] + 27 α[14] - 34 β ≥ 47.0
cons[6] : 28 α[1] + 11 α[2] + 27 α[3] + 25 α[4] + 49 α[5] + 13 α[7] + 43 α[9] + 11 α[10] + 34 α[11] + 23 α[12] + 33 α[14] - 7 β ≥ 0.0
cons[7] : 33 α[1] + 38 α[4] + 39 α[5] + 6 α[7] + 47 α[8] + 20 α[11] + 19 α[14] + 29 β ≥ 0.0
cons[8] : 22 α[3] + 26 α[5] + 37 α[8] + 48 α[9] + 21 α[10] + 38 α[12] + 36 α[13] + 40 α[14] - β ≥ 9.0
cons[9] : 41 α[1] + 5 α[2] + 30 α[3] + 14 α[4] + 10 α[5] + 31 α[8] + 9 α[9] + 11 α[10] + 49 α[12] + 36 α[14] + 36 β ≥ 19.0
cons[10] : 46 α[1] + 4 α[2] + 31 α[4] + 40 α[5] + 36 α[6] + α[7] + 22 α[8] + 21 α[10] + 14 α[11] + 37 α[13] + 34 α[14] - 19 β ≥ 1.0
cons[11] : 15 α[1] + 42 α[3] + 3 α[4] + 19 α[5] + 38 α[6] + 24 α[7] + 17 α[8] + 35 α[9] + 41 α[10] + 5 α[13] + 8 α[14] + 44 β ≥ 0.0
cons[12] : 47 α[1] + 36 α[3] + 31 α[5] + 6 α[8] + 14 α[9] + 8 α[10] + 20 α[12] + 44 α[13] + 4 β ≥ 35.0
cons[13] : 5 α[1] + 9 α[3] + 23 α[4] + 21 α[5] + 19 α[6] + 8 α[7] + 8 α[8] + 5 α[9] + 2 α[10] + 22 α[12] + 22 α[13] + 43 α[14] - β ≥ 5.0
cons[14] : 25 α[1] + 11 α[4] + 42 α[5] + 28 α[7] + 46 α[8] + 48 α[9] + 37 α[10] + 25 α[11] + 38 α[12] + 46 α[13] + 19 α[14] + 16 β ≥ 0.0
cons[15] : 36 α[1] + 21 α[3] + 2 α[5] + 41 α[8] + α[9] + 49 α[10] + 19 α[11] + 32 α[13] + 23 α[14] + 30 β ≥ 0.0
α[1] ≥ 0.0
α[2] ≥ 0.0
α[3] ≥ 0.0
α[4] ≥ 0.0
α[5] ≥ 0.0
α[6] ≥ 0.0
α[7] ≥ 0.0
α[8] ≥ 0.0
α[9] ≥ 0.0
α[10] ≥ 0.0
α[11] ≥ 0.0
α[12] ≥ 0.0
α[13] ≥ 0.0
α[14] ≥ 0.0
β ≥ 0.0 |
|
I also run into numerical inconsistency and want to play with the value of |
|
@sebastiendesignolle I think this was with an old build system. With the new one, you should override the artifact location for cddlib_jll: |
|
The UUID to override is here: |
|
in a file |
|
Thanks @matbesancon, it's working perfectly now! Minor note: building cdd from its source puts the files that julia is looking for in |
|
Is there anything actionable to do here? I don't think we should compile with a different value, and the overrides work. |
|
It indeed seems all good to me, thanks! |
|
for the long term, we could transfer the issue to the lib itself to make this a runtime parameter? |
|
There is cddlib/cddlib#34, but it doesn't explicitly ask for it to be a parameter |


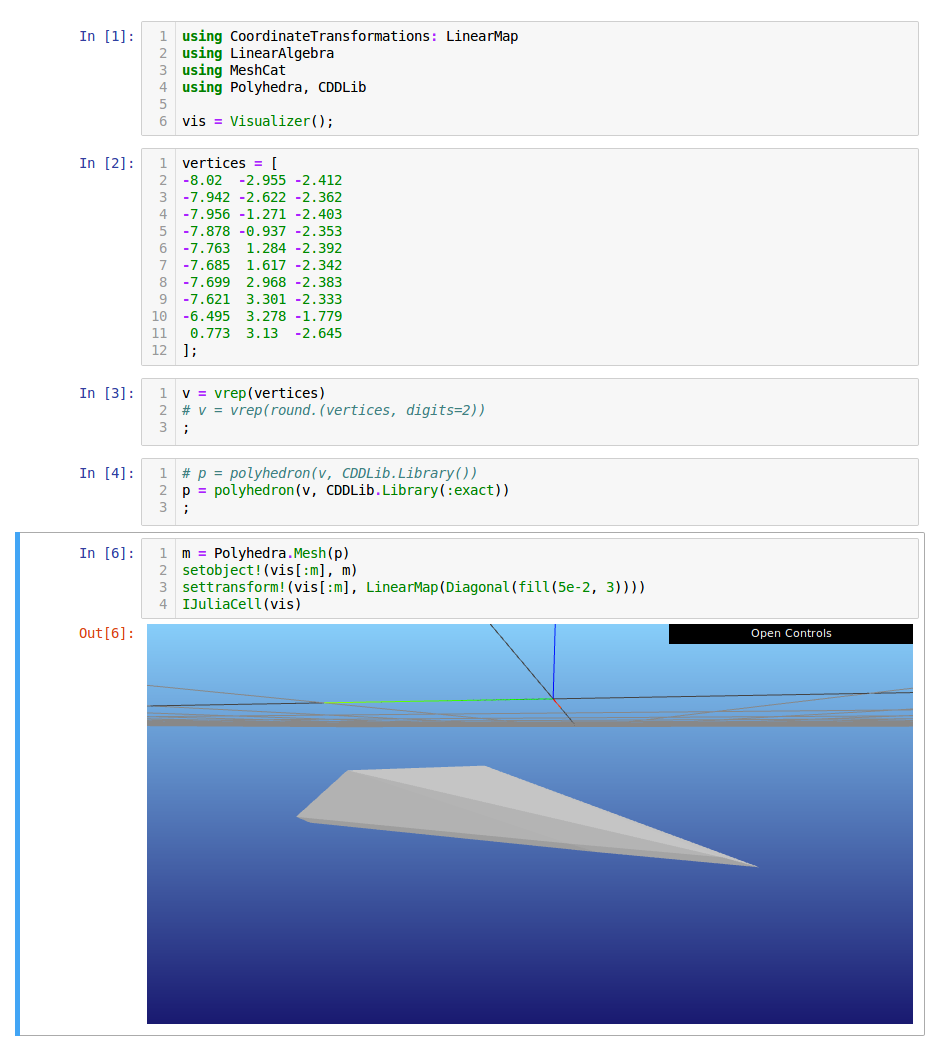
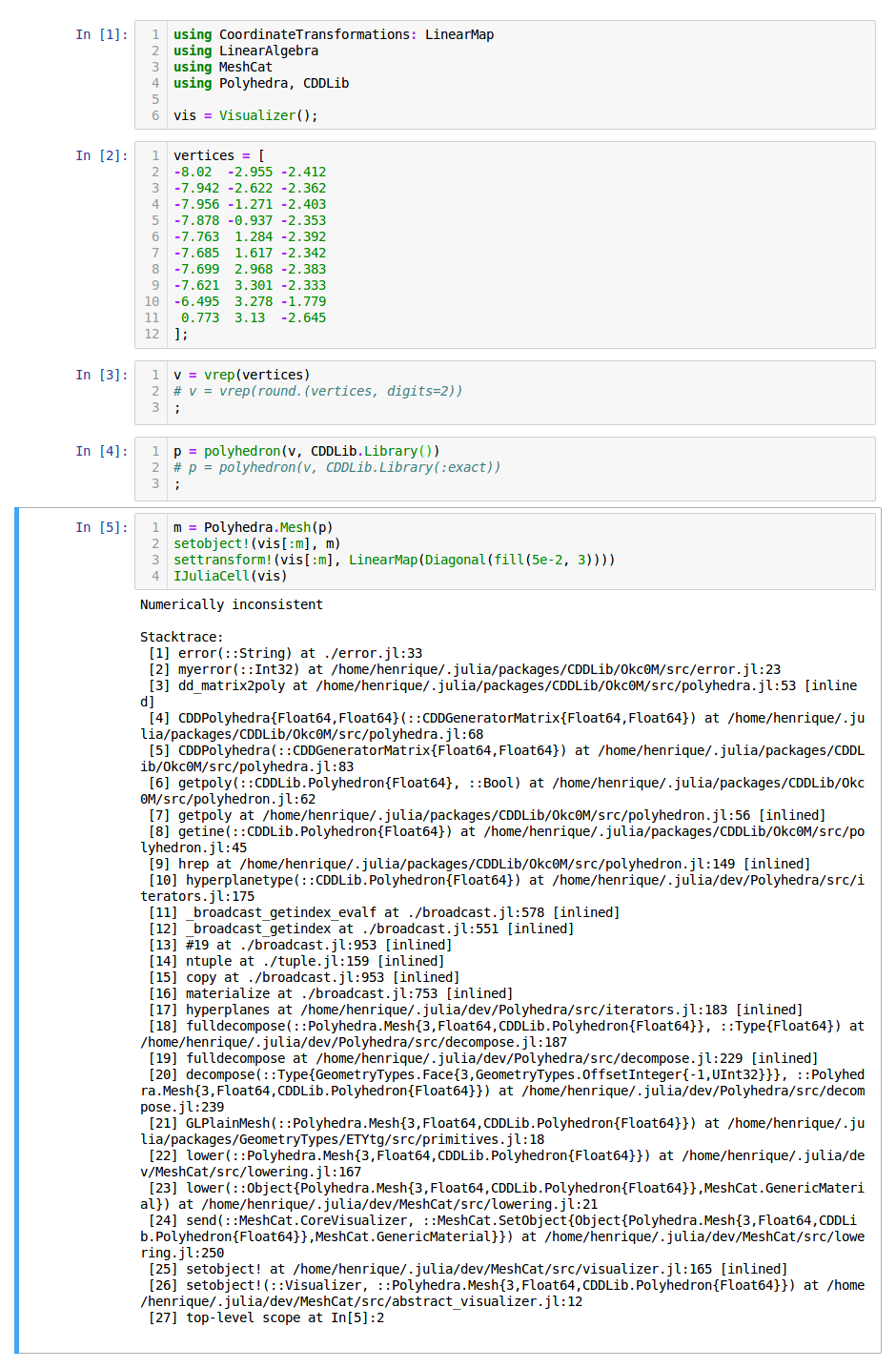
I would like to understand why I sometimes run into a numerical inconsistency.
For example, take a 3D shape defined by the following vertices:
Now, if I try to create a mesh from those vertices with
I will end up with the following error:
Using exact arithmetic seems to get rid of this issue but at the cost of extreme computational times:
Screenshots of a notebook showing both situations:
With exact arithmetic:
Without exact arithmetic:
The text was updated successfully, but these errors were encountered: