参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

209.长度最小的子数组

力扣题目链接

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

提示：

1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5

思路

为了易于大家理解，我特意录制了B站视频拿下滑动窗口！ | LeetCode 209 长度最小的子数组，结合视频看本题解，事半功倍！

暴力解法

这道题目暴力解法当然是两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)。

代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

后面力扣更新了数据，暴力解法已经超时了。

滑动窗口

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入暴力解法的怪圈。

所以只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。

那么问题来了，滑动窗口的起始位置如何移动呢？

这里还是以题目中的示例来举例，s=7，数组是 2，3，1，2，4，3，来看一下查找的过程：

最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

窗口就是满足其和 ≥ s 的长度最小的连续子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

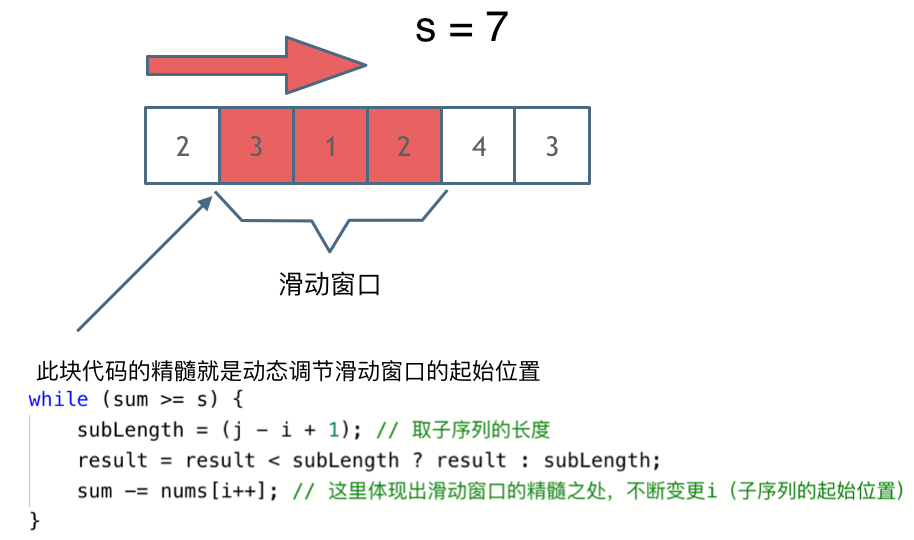
解题的关键在于窗口的起始位置如何移动，如图所示：

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

C++代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

一些录友会疑惑为什么时间复杂度是O(n)。

不要以为for里放一个while就以为是O(n^2)啊，主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。

其他语言版本

Java：

class Solution {

    // 滑动窗口
    public int minSubArrayLen(int s, int[] nums) {
        int left = 0;
        int sum = 0;
        int result = Integer.MAX_VALUE;
        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= s) {
                result = Math.min(result, right - left + 1);
                sum -= nums[left++];
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

Python：

class Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        res = float("inf")   # 定义一个无限大的数
        Sum = 0     # 滑动窗口数值之和
        i = 0      # 滑动窗口起始位置
        for j in range(len(nums)):
            Sum += nums[j]
            while Sum >= s:
                res = min(res, j-i+1)
                Sum -= nums[i]
                i += 1
        return 0 if res == float("inf") else res

Go：

func minSubArrayLen(target int, nums []int) int {
    i := 0
    l := len(nums)  // 数组长度
    sum := 0        // 子数组之和
    result := l + 1 // 初始化返回长度为l+1，目的是为了判断“不存在符合条件的子数组，返回0”的情况
    for j := 0; j < l; j++ {
        sum += nums[j]
        for sum >= target {
            subLength := j - i + 1
            if subLength < result {
                result = subLength
            }
            sum -= nums[i]
            i++
        }
    }
    if result == l+1 {
        return 0
    } else {
        return result
    }
}

JavaScript:

var minSubArrayLen = function(target, nums) {
    let start, end
    start = end = 0
    let sum = 0
    let len = nums.length
    let ans = Infinity
    
    while(end < len){
        sum += nums[end];
        while (sum >= target) {
            ans = Math.min(ans, end - start + 1);
            sum -= nums[start];
            start++;
        }
        end++;
    }
    return ans === Infinity ? 0 : ans
};

Typescript：

function minSubArrayLen(target: number, nums: number[]): number {
    let left: number = 0, right: number = 0;
    let res: number = nums.length + 1;
    let sum: number = 0;
    while (right < nums.length) {
        sum += nums[right];
        if (sum >= target) {
            // 不断移动左指针，直到不能再缩小为止
            while (sum - nums[left] >= target) {
                sum -= nums[left++];
            }
            res = Math.min(res, right - left + 1);
        }
        right++;
    }
    return res === nums.length + 1 ? 0 : res;
};

Swift:

func minSubArrayLen(_ target: Int, _ nums: [Int]) -> Int {
    var result = Int.max
    var sum = 0
    var starIndex = 0
    for endIndex in 0..<nums.count {
        sum += nums[endIndex]

        while sum >= target {
            result = min(result, endIndex - starIndex + 1)
            sum -= nums[starIndex]
            starIndex += 1
        }
    }

    return result == Int.max ? 0 : result
}

Rust:

impl Solution {
    pub fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
        let (mut result, mut subLength): (i32, i32) = (i32::MAX, 0);
        let (mut sum, mut i) = (0, 0);

        for (pos, val) in nums.iter().enumerate() {
            sum += val;
            while sum >= target {
                subLength = (pos - i + 1) as i32;
                if result > subLength {
                    result = subLength;
                }
                sum -= nums[i];
                i += 1;
            }
        }
        if result == i32::MAX {
            return 0;
        }
        result
    }
}

PHP:

// 双指针 - 滑动窗口
class Solution {
    /**
     * @param Integer $target
     * @param Integer[] $nums
     * @return Integer
     */
    function minSubArrayLen($target, $nums) {
        if (count($nums) < 1) {
            return 0;
        }
        $sum = 0;
        $res = PHP_INT_MAX;
        $left = 0;
        for ($right = 0; $right < count($nums); $right++) {
            $sum += $nums[$right];
            while ($sum >= $target) {
                $res = min($res, $right - $left + 1);
                $sum -= $nums[$left];
                $left++;
            }
        }
        return $res == PHP_INT_MAX ? 0 : $res;
    }
}

Ruby:

def min_sub_array_len(target, nums)
  res = Float::INFINITY # 无穷大
  i, sum = 0, 0
  nums.length.times do |j|
    sum	+= nums[j]
    while sum >= target
      res = [res, j - i + 1].min
      sum -= nums[i]
      i	+= 1
    end
  end
  res == Float::INFINITY ? 0 : res
end

C: 暴力解法:

int minSubArrayLen(int target, int* nums, int numsSize){
    //初始化最小长度为INT_MAX
    int minLength = INT_MAX;
    int sum;

    int left, right;
    for(left = 0; left < numsSize; ++left) {
        //每次遍历都清零sum，计算当前位置后和>=target的子数组的长度
        sum = 0;
        //从left开始，sum中添加元素
        for(right = left; right < numsSize; ++right) {
            sum += nums[right];
            //若加入当前元素后，和大于target，则更新minLength
            if(sum >= target) {
                int subLength = right - left + 1;
                minLength = minLength < subLength ? minLength : subLength;
            }
        }
    }
    //若minLength不为INT_MAX，则返回minLnegth
    return minLength == INT_MAX ? 0 : minLength;
}

滑动窗口:

int minSubArrayLen(int target, int* nums, int numsSize){
    //初始化最小长度为INT_MAX
    int minLength = INT_MAX;
    int sum = 0;

    int left = 0, right = 0;
    //右边界向右扩展
    for(; right < numsSize; ++right) {
        sum += nums[right];
        //当sum的值大于等于target时，保存长度，并且收缩左边界
        while(sum >= target) {
            int subLength = right - left + 1;
            minLength = minLength < subLength ? minLength : subLength;
            sum -= nums[left++];
        }
    }
    //若minLength不为INT_MAX，则返回minLnegth
    return minLength == INT_MAX ? 0 : minLength;
}

Kotlin:

class Solution {
    fun minSubArrayLen(target: Int, nums: IntArray): Int {
        var start = 0
        var end = 0
        var ret = Int.MAX_VALUE
        var count = 0
        while (end < nums.size) {
            count += nums[end]
            while (count >= target) {
                ret = if (ret > (end - start + 1)) end - start + 1 else ret
                count -= nums[start++]
            }
            end++
        }
        return if (ret == Int.MAX_VALUE) 0 else ret
    }
}

滑动窗口

class Solution {
   fun minSubArrayLen(target: Int, nums: IntArray): Int {
    // 左边界 和 右边界
    var left: Int = 0
    var right: Int = 0
    // sum 用来记录和
    var sum: Int = 0
    // result记录一个固定值，便于判断是否存在的这样的数组
    var result: Int = Int.MAX_VALUE
    // subLenth记录长度
    var subLength = Int.MAX_VALUE
   

    while (right < nums.size) {
        // 从数组首元素开始逐次求和
        sum += nums[right++]
        // 判断
        while (sum >= target) {
            var temp = right - left 
            // 每次和上一次比较求出最小数组长度
            subLength = if (subLength > temp) temp else subLength
            // sum减少，左边界右移
            sum -= nums[left++]
        }
    }
    // 如果subLength为初始值，则说明长度为0，否则返回subLength
    return if(subLength == result) 0 else subLength
    }
}

Scala:

滑动窗口:

object Solution {
  def minSubArrayLen(target: Int, nums: Array[Int]): Int = {
    var result = Int.MaxValue // 返回结果，默认最大值
    var left = 0 // 慢指针，当sum>=target，向右移动
    var sum = 0 // 窗口值的总和
    for (right <- 0 until nums.length) {
      sum += nums(right)
      while (sum >= target) {
        result = math.min(result, right - left + 1) // 产生新结果
        sum -= nums(left) // 左指针移动，窗口总和减去左指针的值
        left += 1 // 左指针向右移动
      }
    }
    // 相当于三元运算符，return关键字可以省略
    if (result == Int.MaxValue) 0 else result
  }
}

暴力解法:

object Solution {
  def minSubArrayLen(target: Int, nums: Array[Int]): Int = {
    import scala.util.control.Breaks
    var res = Int.MaxValue
    var subLength = 0
    for (i <- 0 until nums.length) {
      var sum = 0
      Breaks.breakable(
        for (j <- i until nums.length) {
          sum += nums(j)
          if (sum >= target) {
            subLength = j - i + 1
            res = math.min(subLength, res)
            Breaks.break()
          }
        }
      )
    }
    // 相当于三元运算符
    if (res == Int.MaxValue) 0 else res
  }
}

C#:

public class Solution {
    public int MinSubArrayLen(int s, int[] nums) {
        int n = nums.Length;
        int ans = int.MaxValue;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n)  {
            sum += nums[end];
            while (sum >= s) 
            {
                ans = Math.Min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == int.MaxValue ? 0 : ans;
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

0209.长度最小的子数组.md

0209.长度最小的子数组.md

209.长度最小的子数组

思路

暴力解法

滑动窗口

相关题目推荐

其他语言版本

Files

0209.长度最小的子数组.md

Latest commit

History

0209.长度最小的子数组.md

File metadata and controls

209.长度最小的子数组

思路

暴力解法

滑动窗口

相关题目推荐

其他语言版本