You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Hi
Great work! Your paper gave me a lot of inspiration. I encountered a problem during reading. I would like to ask you to help me understand the Eq.(4)(5)(6). Specifically, why (4) can be directly derived (5) and (6). I guess it should be because I don't know much about the characteristics of the Jacobian. Since I am just getting started, I don't know what basic knowledge should be searched to further understand this Eq, so I would like to ask for your help.
The text was updated successfully, but these errors were encountered:
The absolute value of the partial derivative term is the determinant of the jacobian matrix. This can be obtained by considering the derivative of the CDF $P(\cdot)$.
Let X be a random variable ($\tilde{z}^a$$\tilde{z}^b$ in the paper) and $z=T^{-1}(x)$, if T is a monotonically increasing function (similar in the decreasing case), then
$\begin{align} P(Z \leq z) = P(T^{-1}(X) \leq z) = P(X \leq T(z)) \end{align}$.
Deriving both sides of the equation,
$\begin{align} p(z) = \pm p(T(z)) \frac{\partial T(z)}{\partial z} = p(x) \left\lvert \frac{\partial x}{\partial z}\right\rvert = \left\lvert T^{\prime}(x)\right\rvert p(T(x)) \end{align}$.
Hi
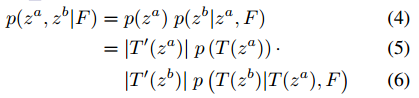
Great work! Your paper gave me a lot of inspiration. I encountered a problem during reading. I would like to ask you to help me understand the Eq.(4)(5)(6). Specifically, why (4) can be directly derived (5) and (6). I guess it should be because I don't know much about the characteristics of the Jacobian. Since I am just getting started, I don't know what basic knowledge should be searched to further understand this Eq, so I would like to ask for your help.
The text was updated successfully, but these errors were encountered: