22.括号生成.md

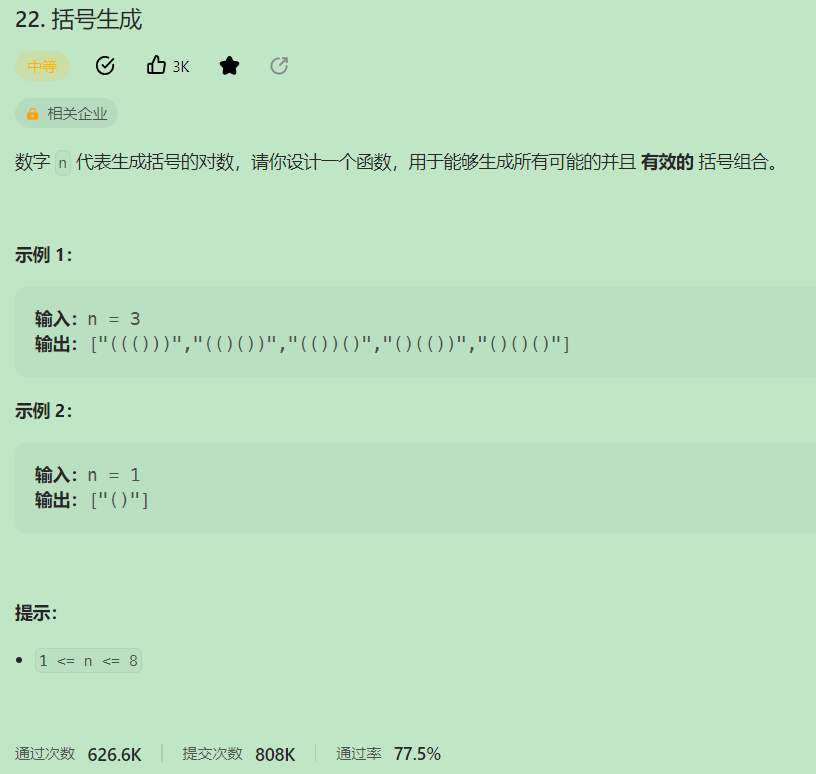
// 复习 
// 重新做时的题解

class Solution {
public:
    void backTrack(int num_l, int num_r, int n) {
        if (com.size() == 2 * n) {
            coms.push_back(com);
            return;
        }

        if (num_l < n) {
            com.push_back('(');
            // num_l++和num_l--是一个随递归过程记录的标志状态，和sum类似，注意写法。
            num_l++;
            backTrack(num_l, num_r, n);
            com.pop_back();
            num_l--;
        }

        if (num_r < n && num_r < num_l) {
            com.push_back(')');
            num_r++;
            backTrack(num_l, num_r, n);
            com.pop_back();
            num_r--;
        }
    }

    vector<string> generateParenthesis(int n) {
        backTrack(0, 0, n);
        return coms;
    }

    vector<string> coms;
    string com;
};

// 回溯里面较难的一题，首先可能能够想到用回溯来解，然后就不知道怎么办了，这是括号问题回溯的特殊之处。
// 举例：对于4个括号，2左2右，则一共只有()()和(())两种可能。
// 对于经典的n=4，k=2的组合回溯问题，从1234个数里选2个组合，那么要选两次，画出回溯树，一共就是2层，第1层选第一个数，第2层选第2个数。
// 回溯树的高度，是递归的次数，回溯树的宽度，是当前层的递归函数，要去处理几次（即当前层调backTrack几次）对于上述问题，通常是用一个for()循环来解决当前层的多次调用backTrack()。

// 对于此题也是类似，括号一共有2种选择，一共要选4次（即n=2，k=4），但其难点在于，选的过程是有限制条件的，这会体现在每层的递归上，即每层的多个backTrack不一定都能执行。
// 且这种回溯显然不写for()来循环处理每层的backTrack()，所以按顺序写，因此就有以下模板：
// if (con1) 什么条件时，可以放置左括号
//     backTrack() 放置左括号
// if (con2) 什么条件时，可以放置右括号
//     backTrack() 放置右括号
// 可见，对于n、k这两个数，我们在写递归内部逻辑时，n其实是要关注的（注意这里的n不是说题干的n，是说的种类数，即左or右括号，n=2），这决定了我们当前层要处理几次backTrack()。
// 而对于k（即此时的4，即题干的n比如为2时，k=2*2，一共放置4个括号，每次放1个，则要递归4层），k其实在递归内逻辑不需要关注，而是需要在“终止条件”关注！这决定了我们什么时候停止递归。

class Solution {
public:
    void backTrack(vector<string>& coms, string com, int left, int right, int n) {
        // k决定递归的深度，决定一共放置几个括号，比如4个，决定终止条件。
        if (com.size() == n * 2) {
            coms.push_back(com);
            return;
        }

        // backTrack在当前层的出现次数，决定当前层递归要处理的种类数，即处理backTrack的次数，即当前层有2种括号可以放置，即左or右。
        // backTrack的限制条件，是本题的难点。
        if (left < n) {
            com.push_back('(');
            // left+1和上面的num_l++/--都是可行的，主要目的是标志当前层的num_l，两种写法都行。
            backTrack(coms, com, left + 1, right, n);
            com.pop_back();
        }

        if (right < left) {
            com.push_back(')');
            backTrack(coms, com, left, right + 1, n);
            com.pop_back();
        }
    }

    vector<string> generateParenthesis(int n) {
        // coms、com是回溯模板的重要存在。
        // 结合n、k想清楚当前层种类数、递归深度终止条件，这类题就能迎刃而解。
        vector<string> coms;
        string com;
        backTrack(coms, com, 0, 0, n);
        return coms;
    }
};