在实现3D地球时,球面是通过地理贴图渲染的。所以我们所说的地理坐标和三维空间坐标的转换,是指将地理贴图上的坐标,转换为球面坐标,即three.js中的三维坐标。
在介绍他们之间如何转换之前,我们先来了解下这两种坐标。
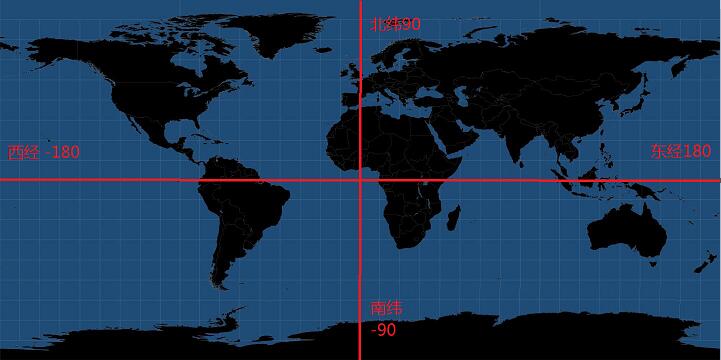
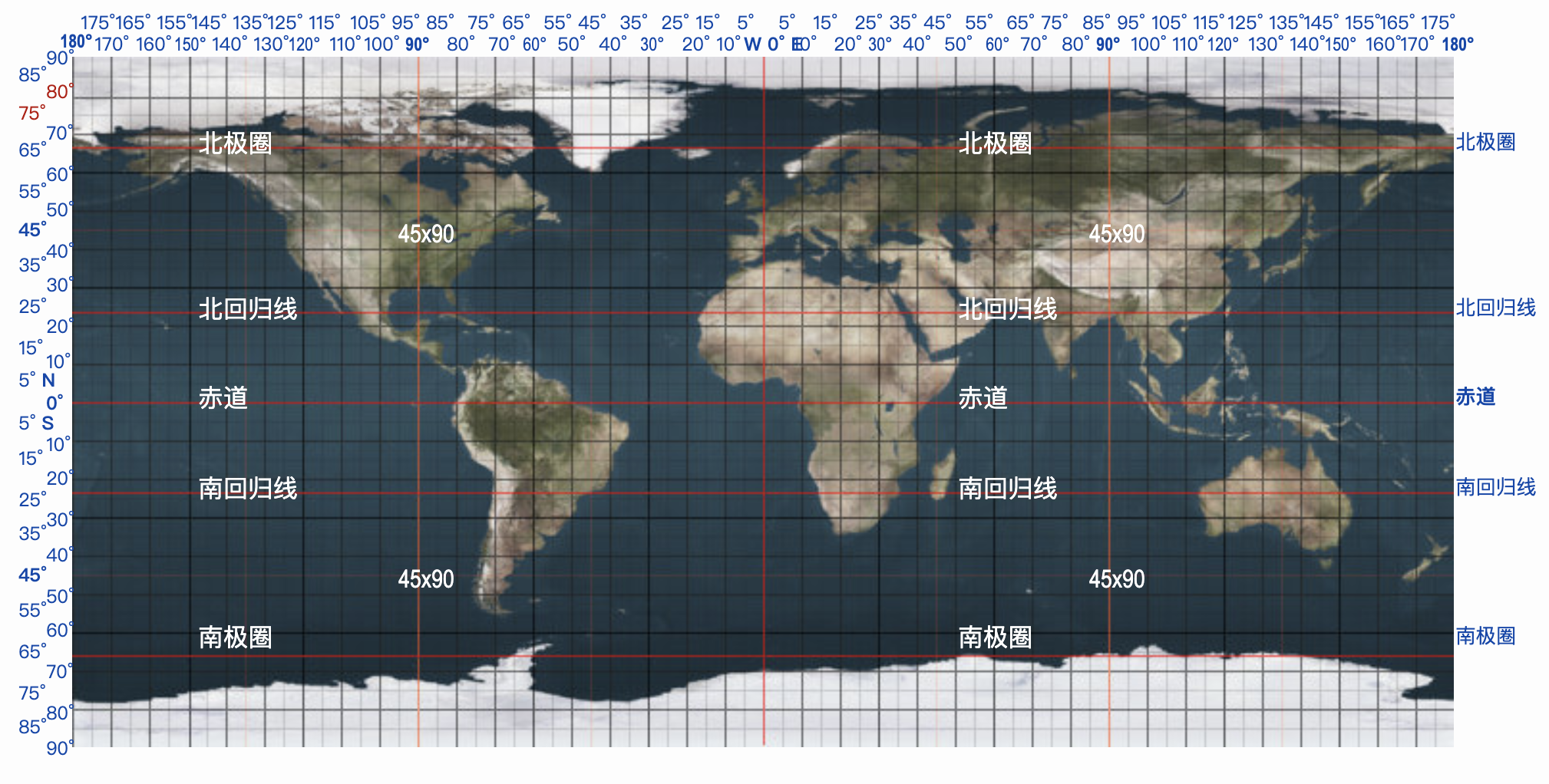
一个完整的地理贴图坐标如下,其中第一张为简图,能够帮我们快速理解经纬度与地理坐标,第二张为详细经纬度分布图。
可以看出贴图横向表示经度,范围**[-180(西经),180(东经)],竖向表示纬度[-90(南纬), 90(北纬)]**,因此坐标转化就成了经纬度到球面坐标的转化。
在three.js中,创建球体时有以下几个重要参数:
- 半径(radius)以及分段数
- 水平方向起始角度(phiStart)
- 水平方向角度大小(phiLength)
- 垂直方向起始角(thetaStart)
- 垂直方向角度大小(thetaLength)
其中phiStart的默认值0,起始点为x轴负方向。thetaStart的默认值也为0,起始点为z轴正方向。如下图所示:
如上图,其中phi的值为0-Math.PI*2,对应的经度范围为-180到180,所以与经度对应的phi应为180+lng(lng为经度longitude)。theta的值为0-Math.PI,对应的纬度为90到-90,所以与纬度对应的theta值应为90-lat(lat为纬度latitude)。
基于上述得出的经纬度和球体创建时角度的对应关系,结合三角函数,我们应该可以很方便地算出对应的三维坐标,如下:
x = - r * sin(theta) * cos(phi)
y = r * cos(theta)
z = r * sin(theta) * sin(phi)如下转换为JS代码:
function lglt2xyz(lng, lat, radius) {
const phi = (180 + lng) * (Math.PI / 180)
const theta = (90 - lat) * (Math.PI / 180)
return {
x: -radius * Math.sin(theta) * Math.cos(phi),
y: radius * Math.cos(theta),
z: radius * Math.sin(theta) * Math.sin(phi),
}
}除了上述直接用三角函数来算以外,我们也可以通过Three.js中的提供的方式来计算。主要涉及THREE.Spherical和THREE.Vector3。
THREE.Spherical是three.js中的球面坐标类,用法如下:
var spherical = new THREE.Spherical(radius,phi,theta)其中的三个参数含义分别如下:
- radius:半径,默认为1
- phi: 以y轴正方向为起点的垂直方向弧度值,默认0
- theta: 以z轴正方向为起点的水平方向弧度值,默认0
可以看出,这里的球面坐标类与我们在定义球时所用的球面坐标中的角是有区别的。phi和theta与上面恰恰相反。对应关系分别为(加’的为此处的角度):
- phi’ = theta = 90 - lat
- theta’ = phi - 90 = 90 + lng
THREE.Vector3用于表示三维向量,它有一个setFromSpherical的方法,顾名思义,表示可以从球面坐标得到三维向量坐标。其实,three.js中可以可以实现球面坐标和三维坐标的相互转换,THREE.Spherical也存在类似的setFromVector3方法。
综上,通过three.js自带的方法来转换经纬度时可以用以下方法:
lglt2xyz(lng, lat, radius) {
const theta = (90 + lng) * (Math.PI / 180)
const phi = (90 - lat) * (Math.PI / 180)
return (new THREE.Vector3()).setFromSpherical(new THREE.Spherical(radius, phi, theta))
},